W poszukiwaniu podobnych. Od wyzwania do produktu – machine learning w praktyce

Korzystając z serwisów streamingowych lub sklepów online z pewnością spotkaliście się z rekomendacjami utworów czy produktów podobnych do tych, które już widzieliście. Jak działają tego typu serwisy? W tym artykule przedstawimy jeden z mechanizmów stojących za takimi funkcjonalnościami często spotykanymi w nowoczesnych serwisach sieciowych.

Znajdziecie tu przykłady kodu w języku Python z wykorzystaniem biblioteki FAISS (jednej z kilku dostępnych bibliotek tego typu), która umożliwia takie porównania. Takie biblioteki są rdzeniem nowych rozwiązań w obszarze big data i machine learning, które zaczęły pojawiać się na rynku, a są nazywane wektorowymi bazami danych. Są to specjalizowane rozwiązania pozwalające składować wektory – reprezentacje dowolnych obiektów, na których później można w ramach takiej bazy wykonywać operacje. Jak działa takie rozwiązanie, do czego jest przydatne i jak zbudować samemu coś podobnego – o tym poniżej.

Do czego to jest przydatne?

Poszukiwanie podobnych obiektów ma wiele zastosowań, zależnie od tego co jest naszym „obiektem”. Jeżeli jest to dokument tekstowy, strona internetowa czy email to znalezienie podobnych daje nam dodatkowe źródła informacji, duplikaty czy też plagiaty dokumentów. Jeżeli obiektem jest obrazek to zaczyna być jeszcze ciekawsze – możemy dzięki temu znaleźć inne ujęcia tego samego tematu ze zdjęcia czy grafiki. Jeżeli jest to film lub muzyka to pozwala zasugerować interesujące odbiorcę utwory do obejrzenia lub odsłuchania. Jeżeli jest to po prostu produkt, to poszukiwanie podobnych sprowadza się do wspomagania handlu lub możliwości porównywania cen analogicznych produktów, i tak dalej – porównywane mogą być oferty, lokalizacje czy wręcz sami użytkownicy.

Rozwój Machine Learning (uczenia maszynowego) w ostatnich latach pozwolił opracować nowe metody reprezentacji różnych obiektów (zwłaszcza dokumentów tekstowych, obrazów, wideo, dźwięku), które otworzyły zupełnie nowe możliwości porównywania obiektów. Można powiedzieć, że nastąpił skok jakościowy pod względem skuteczności porównywania, a złożyły się na niego dwa czynniki: jakość samej reprezentacji obiektów, oraz możliwości obliczeniowe w sferze porównywania, które umożliwiają porównywanie dziesiątek czy setek milionów obiektów w stosunkowo krótkim czasie – to właśnie umożliwiają wspomniane wyżej wektorowe bazy danych.

Reprezentacja obiektów

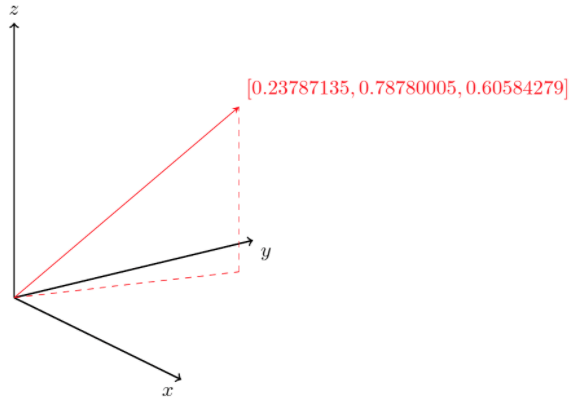
W jaki sposób przedstawić dokumenty, tak aby dało się je porównywać? Potrzebujemy takiego sposobu reprezentacji, który będzie miał następującą własność – obiekty „znaczeniowo podobne” po zaprezentowaniu będą sobie bliskie w jakimś matematycznym sensie (tylko tak potrafimy to wyrazić), a „niepodobne” – odległe. Okazuje się, że dobrym sposobem reprezentacji obiektów jest przedstawienie ich w postaci wektorów, czyli obiektów matematycznych złożonych z wielu liczb. Na wektor można patrzeć jak na punkt w wielowymiarowej przestrzeni (tzw. przestrzeni liniowej). Z punktu widzenia programisty będzie to tablica liczb, na przykład taka:

v = [0.23787135, 0.78780005, 0.60584279]

Jeszcze kilka lat temu każdy wymiar tej przestrzeni wiązano z jakimś pojęciem opisującym reprezentowany obiekt, na przykład jeden z wymiarów reprezentujących dokument mógł odpowiadać temu jak często w dokumencie występuje słowo „piłka”. Każdemu innemu możliwemu słowu odpowiadał inny wymiar. Tego typu reprezentacje okazały się jednak problematyczne ze względu na bardzo dużą liczbę wymiarów i pewną niedokładność reprezentacji widoczną nawet na tym trywialnym przykładzie. Słowo „piłka” może mieć wiele znaczeń (zabawka, narzędzie), które zatracają się w tego rodzaju reprezentacji. Jednak rozwój metod uczenia maszynowego pozwolił odejść od tak dosłownej interpretacji wymiarów – to właśnie element owego skoku jakościowego wspomnianego wyżej.

Zobacz też

AI Jak Netflix wykorzystuje machine learning do wyświetlania filmów?

W nowych rozwiązaniach, zapoczątkowanych pojawieniem się modelu word2vec zachowana jest podstawowa własność – obiekty podobne są bliskimi sobie wektorami (punktami), ale poszczególnych wymiarów nie interpretuje się już jako związanych z konkretnymi pojęciami (słowami lub frazami). Zamiast tego można obliczyć (wytrenować na odpowiednio dużej ilości obiektów porównywanych) takie reprezentacje, które będą w całości zachowywały interesujące podobieństwa znaczeniowe. Jeżeli porównujemy pojedyncze słowa, to cały wektor odpowiada „znaczeniu” słowa. Jeżeli porównujemy zdania lub nawet całe akapity, to cały wektor odpowiada znaczeniom przypisywanym zdaniu czy akapitowi.

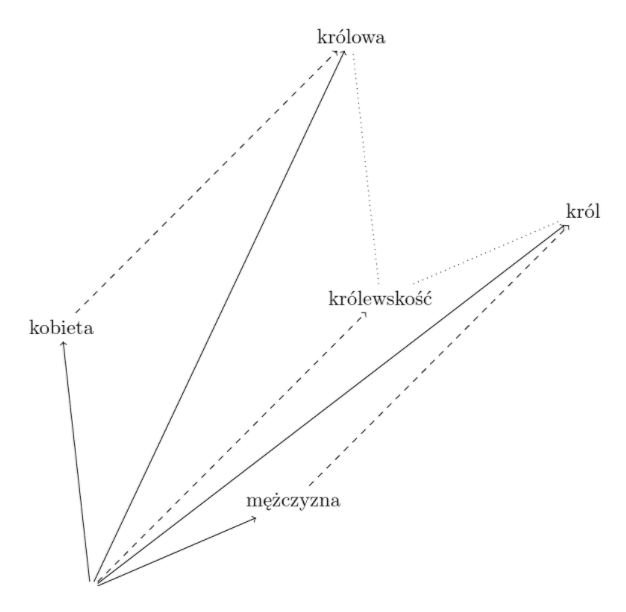
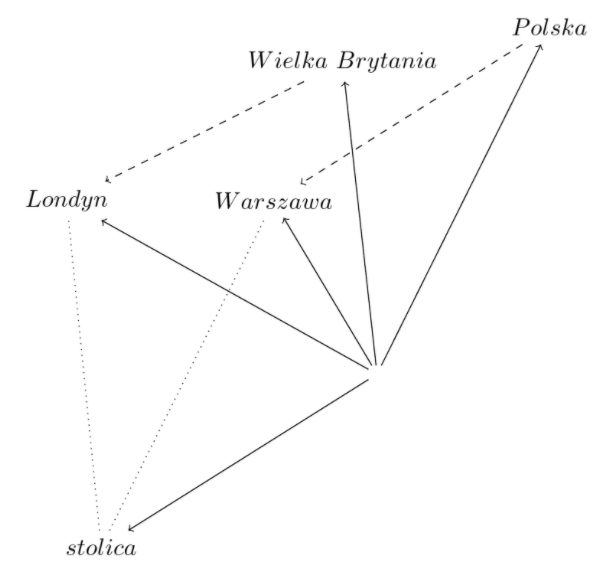
Okazuje się, że jeżeli przeprowadzamy operacje matematyczne na takich wektorach dodając je, czy odejmując, możemy uzyskać ciekawe wyniki „znaczeniowe” – na przykład: jeżeli odejmiemy od wektora reprezentującego słowo „król” wektor reprezentujący „mężczyzna”, a zamiast tego dodamy wektor reprezentujący „kobieta”, to otrzymamy wektor, który leży blisko tego reprezentującego „królowa”. W ten sposób posługujemy się ukrytym, a reprezentowanym w jakiejś postaci w tych wektorach abstrakcyjnym pojęciem „królewskości” obecnym w obu wyrazach „król” i „królowa”. Inny przykład dotyczy np. znaczenia słowa “stolica”, którego wektor można odnieść do innych wektorów oznaczających państwa i ich stolice.

Czytelników zainteresowanych głębiej tym, jak wytrenować sieć neuronową do reprezentacji obiektów mogą zainteresować np. publicznie dostępne modele pozwalające reprezentować w ten sposób zdania. Zamiana dłuższych fragmentów tekstu na reprezentację wektorową (tzw. “paragraph embedding” lub “sentence embedding”) to aktywny temat badań. Jakość tej reprezentacji ma bezpośredni wpływ na to jak dobrze będzie działało nasze rozwiązanie.

Oferty pracy z

W jaki sposób porównywać wektory?

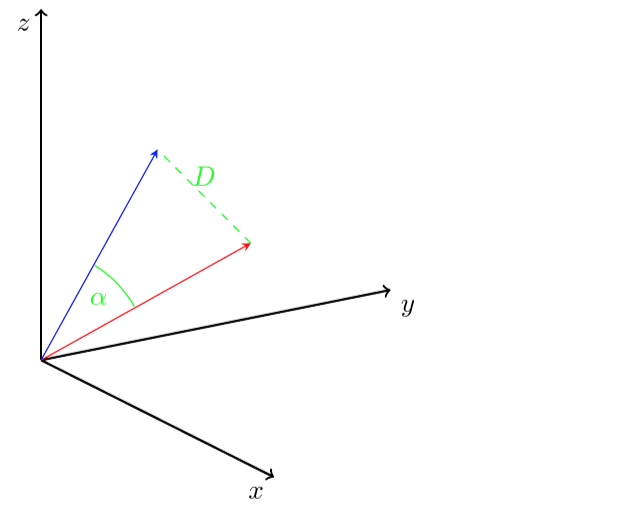
Metoda reprezentowania obiektów przez wektory jest przydatna i łatwa między innymi dlatego, że z matematycznego punktu widzenia potrafimy dobrze określić czym są wektory „podobne”. Możemy posługiwać się różnymi tzw. miarami podobieństwa. Najczęściej spotykane w zastosowaniach to kąt (a właściwie jego cosinus) między wektorami (⍺ na rysunku poniżej), iloczyn skalarny wektorów lub odległość euklidesowa (D na rysunku) zwana także normą L2.

Wektorowe bazy danych umożliwiają wykorzystanie właśnie tych miar do porównywania reprezentacji obiektów. Oprócz nich, dostępne są także w postaci bibliotek open source rozwiązania, których możemy użyć sami do zbudowania porównywarki obiektów. Jednym z nich jest biblioteka FAISS opublikowana przez zespół Facebook AI. Umożliwia ona załadowanie wektorów oraz szukanie podobnych do zadanego wektora z wykorzystaniem standardowych miar podobieństwa.

Przyjrzyjmy się temu jak ją wykorzystać w prostym skrypcie w Pythonie. Oczywiście zanim zaimportujemy potrzebne biblioteki musimy utworzyć pythonowe środowisko i zainstalować w nim kilka przydatnych paczek: faiss-cpu, numpy oraz scikit-learn i matplotlib.

import faiss
from numpy import random, arange, dot
from numpy.linalg import norm

W naszym przykładzie posłużymy się losowymi wektorami, jednakże w realnym zastosowaniu w tym miejscu moglibyśmy zaprząc do pracy oddzielny serwis, który wyliczyłby wektorowe reprezentacje dokumentów, obrazów czy zdań. W przykładzie poniżej posłużymy się realistyczną liczbą wymiarów wektorów (320) – zwykle jest ich kilkaset. Utworzymy też dosyć znaczną ilość wektorów (100 000), która, choć niezbyt duża w porównaniu do spotykanych w rzeczywistości ilości dokumentów, pozwoli nam przekonać się jak szybko działa FAISS.

doc_dimensions_no = 320
number_of_docs = 100_000

random.seed(10234)  # make reproducible

document_vectors = random
   .random((number_of_docs, doc_dimensions_no))
   .astype('float32')
print(document_vectors[:, 0])

Jeżeli chcemy przekonać się jak odległe od siebie są przykładowo wektory o indeksie 0 i 1, możemy wyliczyć ich odległość miarą cosinus wspominaną wyżej.

a = document_vectors[0]
b = document_vectors[1]
cos_sim = dot(a, b)/(norm(a)*norm(b))
print(f"Sim: {cos_sim}")

Kolejny krok to dodanie wektorów do indeksu. Bazę wektorów w terminologii FAISS nazywa się indeksem i w najprostszej wersji, od której tutaj zaczniemy, jest on w całości przechowywany w pamięci RAM. Wykorzystamy na początku indeks płaski, czyli po prostu przechowujący wszystkie wektory bez żadnych przekształceń.

index = faiss.IndexFlatL2(doc_dimensions_no)
index.add(document_vectors)

Mając załadowane do pamięci wektory, możemy przystąpić do odpytywania – wyobraźmy sobie że użytkownik naszego systemu dostarcza nowy dokument. Musielibyśmy wyznaczyć dla niego również wektor reprezentujący (tutaj posłużymy się losowym), a następnie możemy wykorzystać możliwości wyszukiwania oferowane przez FAISS.

number_of_results = 5  # we want to see 5 nearest neighbors
number_of_queries = 1
print(f"Actual search with random {number_of_queries} queries")
query_vectors = random
   .random((number_of_queries, doc_dimensions_no))
   .astype('float32')
# actual search
distances, similar_docs = index.search(query_vectors, number_of_results)
number_of_results_to_present = 5
print(f"First {number_of_results_to_present} results")
print(similar_docs[:number_of_results_to_present])
print(f"Distances of the first {number_of_results_to_present} documents")
print(distances[:number_of_results_to_present])

Wskazaliśmy ile podobnych dokumentów chcemy otrzymać, a dla kontroli lub zastosowania pewnego progu odcięcia możemy uzyskać też odległości między nimi oraz wektorem – zapytaniem.

Dodanie tak małej bazy dokumentów do pamięci trwa około 0.1 sekundy, natomiast wyniki pojedynczego zapytania uzyskamy już w ok. 0.05s (na dosyć przeciętnym komputerze). Jeżeli zwiększymy ilość wektorów do np. 2 mln (a więc 20 razy), to czasy proporcjonalnie wzrosną – ładowanie zabierze ok. 2s, uzyskanie odpowiedzi to już około 1s. To sygnał, że dla naprawdę dużych ilości dokumentów ta metoda może być zbyt wolna. Czy da się szybciej?

FAISS umożliwia podanie wielu takich wektorów w jednym zapytaniu, co przyspiesza działanie w porównaniu do wykonywania pojedynczych zapytań jednego po drugim.

Zobacz też

News Nie uciekniesz przed AI. Algorytm rozpozna cię po stylu pisania

Jednak użycie tak prostego indeksu to dopiero pierwszy etap. FAISS w rzeczywistości wykonuje porównanie naszego zapytania z każdym wektorem przechowywanym w pamięci. Robi to efektywnie, może nawet wykorzystywać do tego możliwości karty graficznej, która jest w istocie procesorem wyspecjalizowanym do obliczeń na wektorach, ale jeżeli tych wektorów jest dużo to takie porównanie musi trwać. Czy można zrobić to lepiej?

Grupowanie wektorów

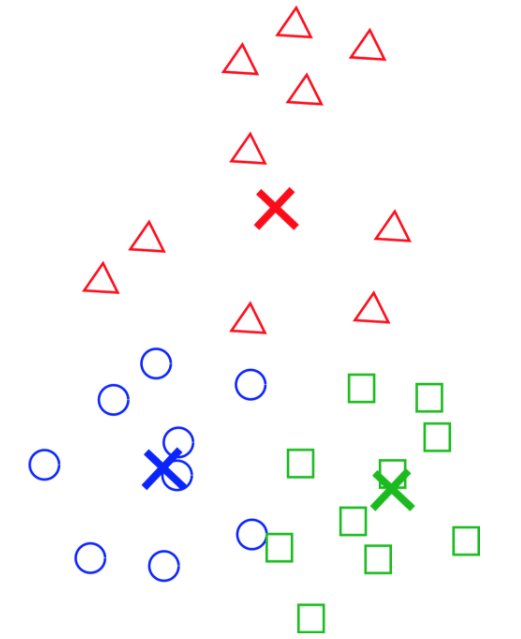
Pierwszym poziomem optymalizacji tego procesu jest wykorzystanie klastrowania (czy też prościej: grupowania) wektorów. Istotą FAISS jest to, że wykorzystuje dobrze znane algorytmy tzw. analizy skupień (klastrowania), aby pogrupować wektory podobne do siebie. Każda taka grupa może być reprezentowana przez jeden wektor, będący na przykład swego rodzaju środkiem wszystkich wektorów z grupy – tak zwany centroid. Wynik działania algorytmu klastrowania można wyobrazić sobie tak jak na rysunku – obiekty (wektory je reprezentujące) przyporządkowane do trzech klastrów wyróżniono kształtem i kolorem, a reprezentanta wyznaczonego dla każdego klastra – jego centroid – oznaczono krzyżykiem.

Jeżeli chcemy odpowiedzieć na zapytanie, to wystarczy je porównać ze stosunkowo niewielką liczbą reprezentantów grup, a następnie dopiero z członkami wybranych już tylko grup, zamiast porównywać zapytanie ze wszystkimi.

Aby to osiągnąć w FAISS musimy wykorzystać inny rodzaj indeksu – taki, który pozwala grupować.

# index preparation
number_of_quantizer_clusters = 100
# the index to hold centroids for partitioning the main index
# it will only hold number_of_quantizer_clusters vectors
quantizer = faiss.IndexFlatL2(doc_dimensions_no)
index = faiss.IndexIVFFlat(quantizer, doc_dimensions_no, number_of_quantizer_clusters)

if not index.is_trained:
   index.train(document_vectors)
assert index.is_trained

Zwróć uwagę, że najpierw przygotowujemy indeks na centroidy, następnie przygotowujemy indeks na właściwe reprezentacje dokumentów, a następnie musimy wykonać tzw. trening indeksu – w tym właśnie momencie odbywa się obliczenie centroidów. Jeżeli dokumentów, z którymi chcemy porównywać jest zbyt dużo, to nie musimy do treningu przekazywać ich wszystkich. Można wykonać próbkowanie, czyli wybrać pewien podzbiór ze wszystkich dokumentów. Centroidy mogą być wówczas gorsze od idealnych, ale czas treningu będzie mieścić się w rozsądnych granicach.

Pozostaje jeszcze załadować wszystkie dokumenty do przygotowanego indeksu. Zostaną one w trakcie ładowania przypisane do wyliczonych centroidów.

index.add(document_vectors)

Odpytywanie tak przygotowanego indeksu odbywa się podobnie jak w przypadku indeksu płaskiego.

Czy użycie takiego indeksu przełożyło się na czas odpowiedzi na zapytanie? Okazuje się, że załadowanie danych do indeksu trwa nieco dłużej (dla 2 mln wektorów to czas ok 5s), jednak czas odpowiedzi na zapytanie bardzo znacznie spadł – do około 0.02s. Tego typu rozwiązanie nadaje się więc do porównywania nawet milionów reprezentacji.

Można też dowiedzieć się jak wyglądają centroidy, które zostały wytrenowane.

centroids = quantizer.reconstruct_n(0, quantizer.ntotal)

print(f"{len(centroids)} centroids found")
print(f"centroids shape {centroids.shape}")
print("First 5 centroids:")
print(centroids[5:])

Jeżeli chcemy ocenić, jak bliskie są sobie centroidy, czyli uzyskać swego rodzaju obraz przestrzeni dokumentów, to także da się łatwo osiągnąć. Wykorzystamy do tego możliwości innego pakietu pythonowego – scipy, i wyrysujemy z jego pomocą dendrogram, czyli drzewo tego jak bliskie sobie są poszczególne grupy dokumentów.

from scipy.cluster.hierarchy import cut_tree, dendrogram, linkage, to_tree
from matplotlib import pyplot as plt

linked = linkage(centroids, 'complete')
labelList = range(0, len(centroids))
plt.figure(figsize=(20, 16))
dendrogram(linked,
          show_contracted=True,truncate_mode='level',p=9,
           orientation='top',
           labels=labelList,
           distance_sort='descending',
           show_leaf_counts=True)
plt.show()

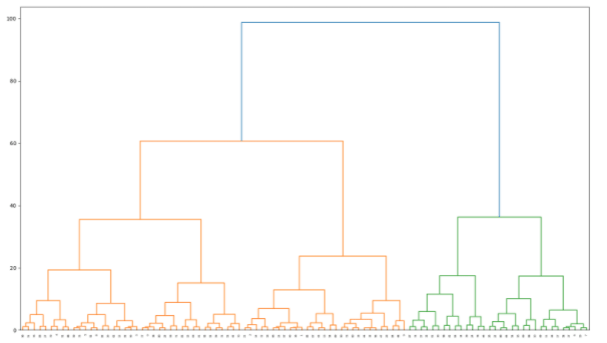Wysokość na rysunku wskazuje na podobieństwo do siebie poszczególnych grup dokumentów (reprezentowanych przez wytrenowany wcześniej centroid).

Podsumowanie

Na tym jednak nie kończą się możliwości biblioteki FAISS ani, tym bardziej, wyzwania stojące przed serwisem porównującym dokumenty. W kolejnym artykule zajmiemy się tym, co zrobić, jeżeli dokumentów jest tak dużo, że ich wektorowe reprezentacje nie mieszczą się w pamięci, a mimo to chcemy je porównywać. Jeżeli chcemy przedstawioną wyżej technikę zastosować w rzeczywiście działającej usłudze, często zderzymy się właśnie z takim problemem – utrzymywanie wszystkiego w pamięci byłoby po prostu zbyt kosztowne lub technicznie niemożliwe.

Zdjęcie główne artykułu pochodzi z unsplash.com.