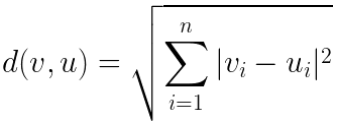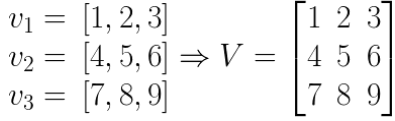Wysokowydajne obliczenia w Pythonie

W tym artykule zaprezentuję koncept wektoryzacji za pomocą biblioteki NumPy. Będziemy testować wiele podejść do efektywnego obliczania odległości euklidesowe pomiędzy dwoma wektorami. Zaczniemy od wyjaśnienia tego czym jest NumPy, czym wektoryzacja, a czym odległość euklidesowa.
Piotr Skoroszewski. Data Scientist w Semantive. Ma doświadczenie w projektowaniu i zarządzaniu systemem przetwarzania dużych danych, programista z dobrą znajomością systemu UNIX, zaplecza Pythona i C ++. Magister informatyki na Uniwersytecie Warszawskim ze specjalnością sztuczna inteligencja i baza danych. Piotr jest jednym z autorów firmowego bloga, a jego hobby to kolarstwo górskie.
Spis treści
Czym jest NumPy?
NumPy jest Pythonową biblioteką przeznaczoną do efektywnego przetwarzania wielowymiarowych macierzy. Jest również bardzo poręcznym narzędziem dla analityków danych, ponieważ zawiera wysokopoziomowe funkcje pracujące na macierzach. Więc jak wykorzystać NumPy do przyspieszenia naszej aplikacji? Odpowiedź to wektoryzacja!
Co to jest wektoryzacja?
Wielkim atutem NumPy jest to, że wykonuje ona iterację na elementach macierzy w ‘warstwie C’, aniżeli w samym Pythonie. Interpreter Pythona jest o rząd wielkości wolniejszy niż programy napisane w C, więc sensowna jest transformacja różnego rodzaju pętli, które iterują po elementach macierzy, na wywołania funkcji w NumPy. Taki zabieg nazywamy wektoryzacją. Zobaczmy jak to wygląda w praktyce.
Odległość euklidesowa
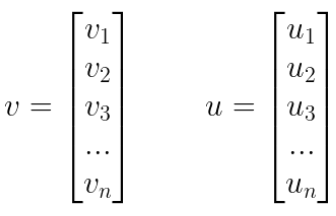
Odległość euklidesowa jest podstawowym terminem w matematyce, więc nie będziemy wchodzić w szczegóły. Najprościej mówiąc, jest to długość odcinka pomiędzy dwoma punktami w przestrzeni wielowymiarowej. Wzór na odległość euklidesową dwóch wektorów <latex>v, u in R^n</latex> jest następujący:
Zobaczmy teraz, jakie metody można użyć do obliczenia odległości i porównajmy je ze sobą.
Dummy algorithm
Zacznijmy od prostego algorytmu, który nie korzysta z NumPy.
def dummy(v, u):
s = 0
for v_i, u_i in zip(v, u):
s += (v_i - u_i)**2
return s ** 0.5
Ten algorytm jest dokładnym odzwierciedleniem definicji – iterujemy po każdej parze elementów wektorów, wykonujemy na niej obliczenia i sumujemy wyniki pośrednie. Bułka z masłem… Aby być bardziej pro, możemy zapisać to jako one-liner:
def dummy(v, u): return sum((v_i - u_i)**2 for v_i, u_i in zip(v, u))**0.5
Bare Numpy
Przepiszmy teraz powyższy algorytm używając NumPy i wektoryzacji.
import numpy as np def bare_numpy(v, u): return np.sqrt(np.sum((v - u) ** 2))
Jak widać to rozwiązanie jest proste i zwięzłe. Tablice NumPy mają przeciążone operatory arytmetyczne (+, -, *, /, **), więc możemy łatwiej operować na elementach tablic. Zwróć uwagę, że zastąpiliśmy Pythonową funkcję sum funkcją numpy.sum, więc tutaj również zoptymalizowaliśmy niejawne iterowanie po elementach.
Scipy Distance
from scipy.spatial import distance def scipy_distance(v, u): return distance.euclidean(v, u)
Okazuje się, że biblioteka scipy ma wbudowaną funkcję do obliczenia odległości euklidesowej. Wspaniale!
<latex>L^2</latex> Norm
Wnikliwy matematyk na pewno dostrzeże, że odległość euklidesowa dwóch wektorów jest niczym innym jak norma <latex>L^2</latex> ich różnicy.
import numpy as np def l2_norm(v, u): return np.linalg.norm(v - u)
Einsum
Konwencja sumacyjna Einsteina jest eleganckim sposobem do wyrażania typowych operacji na macierzach tj. mnożenie punktowe macierzy, sumowanie po osiach oraz transpozycja. Na pierwszy rzut oka, ta metoda może wydawać się nieprzystępna z powodu skomplikowanej składni, ale okazuje się, że jej implementacja jest bardzo wydajna.
import numpy as np
def einsum(v, u):
z = v - u
return np.sqrt(np.einsum('i,i->', z, z))
W tym przypadku wyrażenie ‘i,i->’ oznacza iloczyn skalarny wektora z z samym sobą.
Benchmark!
Skorzystam z fajnej Pythonowej biblioteki Perfplot do testowania i prezentacji wyników. Zobaczymy jak wyglądają testy na trzech prawdziwych przykładach.
Wektory wielowymiarowe
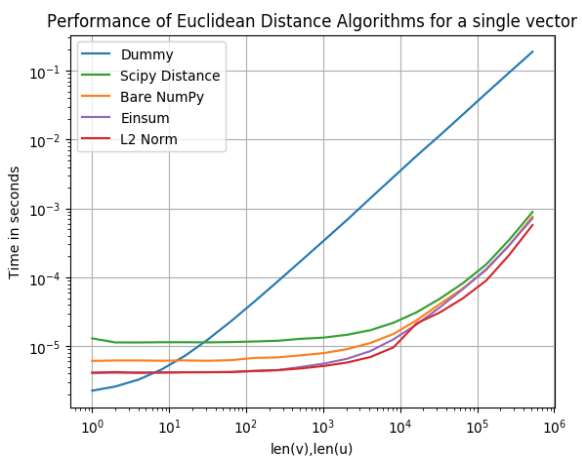
Czasami musimy operować na bardzo długich tablicach, więc porównajmy efektywność algorytmów w zależności od wymiaru wektora v oraz wektora u.
Zaskoczony? Okazuję się, że algorytm Dummy jest nawet 100 razy (!) wolniejszy niż dowolne inne przedstawione podejście. Kształt krzywych dla reszty algorytmów jest bardzo zbliżony i zbiega do tej samej wartości dla coraz większych wymiarów wektora.
Obliczenia na wielu wektorach
W prawdziwych zastosowaniach często trzeba obliczyć odległość euklidesową pomiędzy wieloma wektorami. Przykładowo może mieć to zastosowanie w aplikacjach mapowych do wykonywania operacji na współrzędnych geograficznych. Zamiast obliczać kolejno odległości dla podanych par
wektorów, możemy ponownie skorzystać z wektoryzacji i obliczyć to samo w jednym kroku.
W tym przypadku wektoryzacja polega na zapisaniu wszystkich wektorów w jedną macierz i wykonaniu operacjach na macierzach!
Musimy trochę przerobić nasze funkcje, aby mogły operować na dwuwymiarowych tablicach i voilà:
import numpy as np
def dummy_mat(mat_v, mat_u):
return [sum((v_i - u_i)**2 for v_i, u_i in zip(v, u))**0.5 for v, u in zip(mat_v, mat_u)]
def bare_numpy_mat(mat_v, mat_u):
return np.sqrt(np.sum((mat_v - mat_u) ** 2, axis=1))
def l2_norm_mat(mat_v, mat_u):
return np.linalg.norm(mat_v - mat_u, axis=1)
def scipy_distance_mat(mat_v, mat_u):
# Unfortunately, the scipy_distance only works on 1D-arrays, so we are not able to vectorize it again.
return list(map(distance.euclidean, mat_v, mat_u))
def einsum_mat(mat_v, mat_u):
mat_z = mat_v - mat_u
return np.sqrt(np.einsum('ij,ij->i', mat_z, mat_z))
(Uwaga) scipy_distance operuje wyłącznie na jednowymiarowych tablicach, więc nie jesteśmy w stanie wykonać ponownej wektoryzacji w tym przypadku.
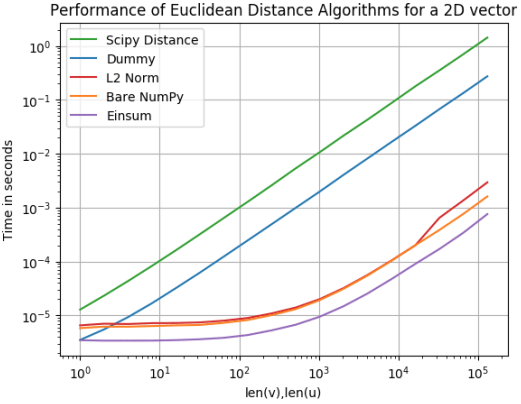
Wiele punktów 2D
Wygląda na to, że nasz algorytm Dummy jest lepszy niż Scipy Distance. Wow! Tyle wygrać! Okazuje się, że Scipy Distance jest najwolniejszy dla punktów 2D oraz 3D. Później zobaczymy jak sobie radzi dla wektorów wielowymiarowych.
Jednak najważniejsze wnioski są następujące:
1. Najszybszym podejściem jest Einsum. Jest o prawie 150 razy szybszy niż Dummy!
2. Bare Numpy jest prawie tak samo szybki jak Einsum pomimo, że Bare Numpy jest bardziej intuicyjny i ma prostszą składnie!
Porównajmy teraz wyniki dla dużo większej liczby wymiarów.
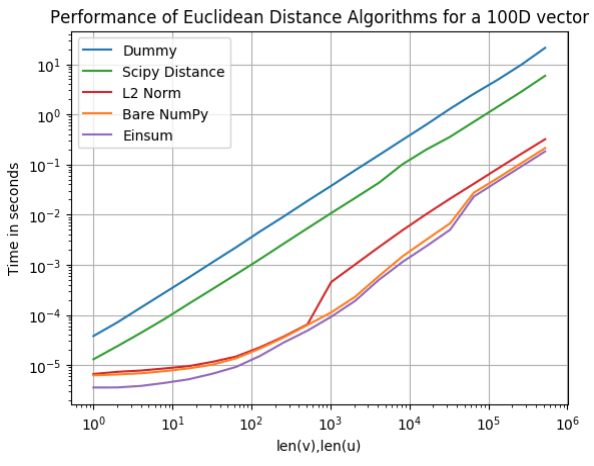
Wiele punktów 100D
Wielowymiarowe wektory są używane do wielu problemów polegających na klastrowaniu np. w algorytm k-NN na danych wielowymiarowych. Naturalnie nie chcemy czekać wieczność na wyniki, więc każda optymalizacja jest na wagę złota. Zobaczymy jak poradziły sobie nasze algorytmy.
Ponownie Einsum okazał się najszybszy, jednak Bare Numpy nie wydaje się sporo gorszy. Na ostatnim miejscu ponownie znalazł się Dummy.
Podsumowanie
Numpy w sposób natywny wspiera wektoryzację, więc nadaje się do szybkiego wykonywania operacji arytmetycznych na macierzach. Numpy ma również bardzo przyjazną składnie, więc łatwo można go używać do poprawienia wydajności swojego programu.
Einsum jest bardzo ciekawym i egzotycznym konceptem i warto go poznać, aby jeszcze bardziej wyżyłować swoje wyniki.
Artykuł został pierwotnie opublikowany na semantive.com. Zdjęcie główne artykułu pochodzi z unsplash.com.
Podobne artykuły

Data wyprzedza JavaScript – nowy lider polskiego rynku IT w 2025
Podejście do zmniejszania kosztów przetwarzania danych na przykładzie Azure Databricks

Data management, data governance i data modernization - jak okiełznać proces zarządzania danymi w organizacji

Big Data - klęska urodzaju czy złoty Graal? Praktyczne metody wykorzystania potencjału danych
Dane 1,3 mln użytkowników Clubhouse do pobrania? To nie wyciek, to data scraping

Text clustering, czyli jak wyciągnąć realną wartość biznesową z milionów wiadomości tekstowych

Migracja do chmury? Wypełnij ankietę i sprawdź, jak wygląda ten proces u innych!