Najczęściej kopiowany fragment kodu na Stack Overflow był wadliwy!

W ostatnim badaniu zatytułowanym Usage and Attribution of Stack Overflow Code Snppets in GitHub Project (pl. Wykorzystanie i przypisanie fragmentów kodu Stack Overflow w projektach GitHub), odpowiedź, którą napisałem niemalże dekadę temu, okazała się najczęściej kopiowanym fragmentem kodu. Jak na ironię jest on uszkodzony.
Andreas Lundblad. Software developer z pasją. Po ukończeniu doktoratu z informatyki dołączył do zespołu langtools w Oracle, gdzie kompilował w Javie i innych narzędziach związanych z językiem. W 2016 roku rozpoczął pracę w Palantir Technologies jako Forward Deployed Engineer. Obecnie zajmuje 10. miejsce na liście 100 najlepszych użytkowników Stack Overflow i został wybrany jako jeden z najlepszych programistów w Szwecji poniżej 30. roku życia. Prowadzi blog programming.guide.
Spis treści
Dawno, dawno temu…
W 2010 roku siedziałem w swoim biurze i robiłem to, czego nie powinienem robić: code golfingowałem i podbijałem reputację na Stack Overflow. Moją uwagę zwróciło następujące pytanie: Jak wydrukować liczbę bajtów w czytelnym dla zwykłego człowieka formacie? To znaczy, jak sformatować coś w stylu 123,456,789 bajtów na “123,5 MB”.
Stary dobry wygląd Stacka z 2010 roku. Można go uzyskać przez Wayback Machine
Łańcuch wynikowy powinien mieć wartość między 1 a 999,9 i poprzedzający go suffix powinien być odpowiedniej wielkości.
Pod zadanym pytaniem znalazła się wówczas jedna odpowiedź. Zawarty w niej kod oparty został na pętli. Pomysł był prosty: wypróbuj wszystkie wielkości od największej (EB= 1018 bajtów) do najmniejszej (B = 1 bajt) i użyj pierwszego, który jest mniejszy niż liczba bajtów. W pseudo-kodzie wygląda to tak:
Zwykle najwyżej punktowaną odpowiedź n Stack Overflow ciężko dogonić. W żargonie określamy to jako Problem Najszybszego Strzelca na Zachodzie (ang. The Fastest Gun in the West Problem). W tym przypadku istniejąca odpowiedź miała kilka wad, więc wciąż widziałem szansę na przebicie jej. W końcu kod oparty na pętli można znacznie uprościć.
To jest przecież algebra, znam więc odpowiedź!
I wtedy do mnie dotarło. kB, MB, GB… Suffixy to nic innego jak moc 1000 (lub 1024 w standardzie IEC), co znaczy, że powinno być możliwe obliczenie odpowiedniego suffixu za pomocą logarytmów zamiast pętli.
Na podstawie tego opublikowałem odpowiedź:
public static String humanReadableByteCount(long bytes, boolean si) {
int unit = si ? 1000 : 1024;
if (bytes < unit) return bytes + " B";
int exp = (int) (Math.log(bytes) / Math.log(unit));
String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp-1) + (si ? "" : "i");
return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre);
}
Fakt, kod nie jest zbyt czytelny, a log / pow prawdopodobnie czyni go mniej wydajnym niż inne rozwiązania, ale nie ma w nim żadnych pętli i prawie żadnych rozgałęzień, co moim zdaniem było całkiem fajne.
Kryjąca się za tym matematyka jest prosta. Liczba bajtów wyrażana jest w byteCount = 1000s, gdzie s oznacza skalę (w przypadku zapisu binarnego używana jest podstawa 1024). Rozwiązanie dla s daje s = log1000 (byteCount).
W interfejsie API nie ma łatwo dostępnego log1000, ale możemy wyrazić go logarytmem naturalnym w następujący sposób: s = log(byteCount) / log(1000). Jeśli dla przykładu mamy więcej niż jeden megabajt (ale nie pełnego gigabajta) i chcemy użyć MB jako wielkości, to sprowadzamy do podłogi s (oddanych do int).
W tym momencie, jeśli s = 1 skala to kilobajty, jeśli s = 2 skala to megabajty i tak dalej. Dzielimy byteCount przez 1000s i wklepujemy odpowiedni prefiks litery.
Po opublikowaniu tego mogłem tylko czekać i sprawdzać, czy społeczność doceni odpowiedź. Nie spodziewałem się, że będzie to najbardziej kopiowany fragment kodu na Stack Overtflow.
Studium na temat atrybucji
W 2018 roku doktorant Sebastian Baltes opublikował artykuł w czasopiśmie Emirical Software Enigneering pt. Usage and Attribution of Stack Overflow Code Snippets in GitHub Projects. I zasadniczo próbuje w nim odpowiedzieć na pytanie: Czy przestrzegana jest licencja Stack Overflow CC BY-SA 3.0? Czyli, w skrócie, czy można korzystać z kodu opublikowanego przez jednego z użytkowników?
Fragmenty kodu dostosowano do kodu ze zrzutu danych Stack Overflow i dopasowano je do kodu z publicznych repozytoriów GitHub. Cytując streszczenie:
Prezentujemy wyniki wielkoskalowego badania empirycznego analizującego wykorzystanie i przypisywanie fragmentów kodu Java z odpowiedzi SO w publicznych projektach GitHub (GH).
(Uwaga, spoiler: Nie. Większość osób nie uwzględnia prawidłowego przypisania)
W artykule znaleźć można następującą tabelę:
Odpowiedź na górze o numerze identyfikacyjnym 3758880 jest właśnie tą odpowiedzią, którą zamieściłem tam osiem lat wcześniej. W tym momencie miała już ponad setki tysięcy wyświetleń i ponad tysiąc pozytywnych opinii.
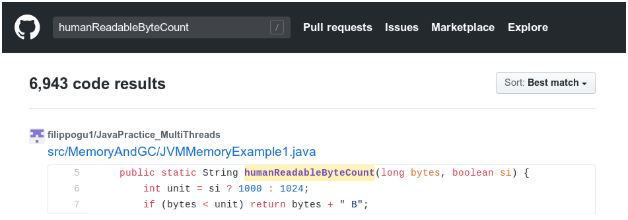
Szybkie wyszukiwanie na GitHub potwierdza, że rzeczywiście kod humanReadableByteCount występuje tysiące razy.
Możesz sprawdzić, czy masz go w lokalnym repozytorium, wpisując komendę:
$ git grep humanReadableByteCount
Bonusowa anegdotka: kiedy po raz pierwszy usłyszałem o tym badaniu?
Sebastian znalazł dopasowanie w repozytorium OpenJDK. Nie było przypisu, a licencja OpenJDK nie była kompatybilna z CC BY-SA 3.0. Sięgnął więc do dev listy mailingowej z zapytaniem, czy kod na Stack Overflow był skopiowany z OpenJDK, czy było to zrobione na odwrót.
Zabawne jest to, że kiedyś pracowałem w Oracle przy projekcie OpenJDK, więc mój były współpracownik i kolega odpisał w następujący sposób:
Cześć,
Dlaczego nie zapytasz autora tego postu (aioobe) bezpośrednio? Jest współpracownikiem OpenJDK i był zatrudniony przez Oracle w momencie pojawienia się tego kodu w repozytoriach źródłowych OpenJDK.
/Claes
Oracle nie lekceważy takich zgłoszeń. Wiem, że niektórzy ludzie z firmy musieli odetchnąć z ulgą, kiedy przeczytali tę odpowiedź i uznali to za drobny triumf po tym „oskarżeniu”.
Po uzyskaniu odpowiedzi, Sebastian zwrócił się do mnie, abym to wyjaśnił, co też zrobiłem. Nie pracowałem w Oracle, kiedy zostało to zatwierdzone i nie włączyłem tej łatki. Piłka po Waszej stronie, Oracle. Krótko po wszystkim problem został naprawiony (https://bugs.openjdk.java.net/browse/JDK-8170860), a kod usunięty (http://hg.openjdk.java.net/jdk9/jdk9/hotspot/rev/b552b596203f).
Błąd
Założę się, że już zacząłeś się zastanawiać. Gdzie jest błąd we fragmencie tego kodu?
Powtórzę:
public static String humanReadableByteCount(long bytes, boolean si) {
int unit = si ? 1000 : 1024;
if (bytes < unit) return bytes + " B";
int exp = (int) (Math.log(bytes) / Math.log(unit));
String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp-1) + (si ? "" : "i");
return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre);
}
Po eksabajtach 1018 przychodzą zettabajty 1021. Czy to możliwe, że naprawdę duże dane wejściowe powodują, że indeks wykracza poza granice „kMGTPE” ciągu? Nie. Maksymalna wartość long wynosi 263 - 1 ≈ 9.2 × 1018, więc żadna wartość long nigdy nie przekroczy wartości EB.
Czy może to być pomieszanie SI i binarnych? Nie. Wczesna wersja odpowiedzi zawierała pomyłkę, ale dość szybko została ona naprawiona.
Czy w końcu exp może być 0, powodując awarię charAt(exp-1)? Pierwsze if-statement koryguję tę sprawę. Wartość exp zawsze będzie wynosić przynajmniej 1.
Czy może to być jakiś dziwny błąd zaokrąglenia na wyjściu? No właśnie.
Wiele dziewiątek
Rozwiązanie działa aż do osiągnięcia 1 MB. Gdy podano 999,999 bajtów jako dane wejściowe, w trybie SI wynikiem jest "1000.0 kB". Chociaż prawdą jest, że 999,999 jest bliższy 1000 x 10001 niż 999,9 x 1000 do 1. 1000 „znaczeń” jest poza zakresem, zgodnie ze specyfikacją. Prawidłowy wynik wynosi"1.0 MB".
Jeśli ma to jakiekolwiek znaczenie, wszystkie 22 opublikowane odpowiedzi, w tym te wykorzystujące biblioteki Apache Commons i Android, miały ten błąd (lub jego odmianę) w momencie pisania.
Jak to naprawić? Przede wszystkim zauważmy, że wykładnik (exp) powinien zmienić się z „k” na „M”, gdy tylko liczba bajtów będzie bliższa 1 × 1,0002 (1 MB) niż 999.9 × 10001 (999,9 k). Dzieje się tak przy 999,950. Podobnie powinniśmy przejść z „M” na „G”, gdy miniemy 999,950 i tak dalej.
Aby to osiągnąć, obliczamy ten próg i wpisujemy, że exp jeśli bytes jest większy:
if (bytes >= Math.pow(unit, exp) * (unit - 0.05))
exp++;
Dzięki tej zmianie kod działa dobrze aż do momentu, gdy liczba bajtów zbliży się do 1 EB.
Jeszcze więcej dziewiątek
Biorąc pod uwagę otrzymane 999,949,999,999,999,999, ukazuje się nam wynik 1000.0 PB, kiedy poprawną odpowiedzią jest 999.9 PB . Pod względem matematycznym kod jest poprawny, więc co właściwie się stało?
W tym momencie natrafiamy na ograniczenia dokładności double.
Arytmetyka zmiennoprzecinkowa 101
Ze względu na IEEE 754, wartości zmiennoprzecinkowe bliskie zeru są bardzo gęste, a duże wartości bardzo rzadkie. W rzeczywistości połowa wszystkich wartości znajduje się między -1 a 1, a gdy mówimy o dużych podwójnych, wartość tak duża jak Long.MAX_VALUE nic nie znaczy. Dosłownie.
double l1 = Double.MAX_VALUE; double l2 = l1 - Long.MAX_VALUE; System.err.println(l1 == l2); // prints true
Więcej o tym w artykule Bits of a Floating Point Value.
Istnieją dwa problematyczne obliczenia:
- Podział argumentu
String.format - Próg uderzenia
exp.
Moglibyśmy przejść na BigDecimal, ale gdzie w tym zabawa? Poza tym i tak robi się bałagan, ponieważ BigDecimal w standardowym interfejsie API nie ma funkcji dziennika.
Skalowanie wartości pośrednich
W przypadku pierwszego problemu możemy zmniejszyć wartość bytes do precyzyjniejszego zakresu i odpowiednio dostosować exp. Końcowy wynik jest zaokrąglany, więc nie ma znaczenia, że wyrzucamy najmniej znaczące cyfry.
if (exp > 4) {
bytes /= unit;
exp--;
}
Dostosowywanie najmniej znaczących bitów
W przypadku drugiej kwestii powinniśmy zadbać o najmniej znaczące bity (999,949,99…9 i 999,950,00… 0 powinny kończyć się różnymi wykładnikami), zatem wymaga to innego rozwiązania.
Po pierwsze, zauważmy, że istnieje 12 różnych możliwości wartości progu (6 dla każdego trybu) i tylko jedna z nich kończy się błędem. Błędny wynik może być jednoznacznie zidentyfikowany przez fakt, że kończy się na D0016. W takim przypadku po prostu dostosowujemy go do prawidłowej wartości.
long th = (long) (Math.pow(unit, exp) * (unit - 0.05));
if (exp < 6 && bytes >= th - ((th & 0xFFF) == 0xD00 ? 52 : 0))
exp++;
Ponieważ polegamy na określonych wzorach bitowych w wyniku zmiennoprzecinkowych, wklepujemy strictfp, żeby upewnić się, że działa niezależnie od sprzętu, na którym działa kod.
Ujemne dane wejściowe
Nie jest jasne, w jakich okolicznościach ujemna liczba bajtów może być istotna, ale ponieważ Java nie ma niepodpisanego long, lepiej sobie z tym poradzić. W tej chwili dane wejściowe takie jak -10 000 dają wynik -10000 B.
Używamy zatem absBytes:
long absBytes = bytes == Long.MIN_VALUE ? Long.MAX_VALUE : Math.abs(bytes);
Skomplikowane wyrażenie wynika z faktu, że -Long.MIN_VALUE == Long.MIN_VALUE. Teraz wykonujemy wszystkie obliczenia związane z używaniem exp absBytes zamiast bytes.
Wersja ostateczna
Oto ostateczna wersja kodu, zgolfowana w duchu ostatecznej wersji:
// From: https://programming.guide/worlds-most-copied-so-snippet.html
public static strictfp String humanReadableByteCount(long bytes, boolean si) {
int unit = si ? 1000 : 1024;
long absBytes = bytes == Long.MIN_VALUE ? Long.MAX_VALUE : Math.abs(bytes);
if (absBytes < unit) return bytes + " B";
int exp = (int) (Math.log(absBytes) / Math.log(unit));
long th = (long) (Math.pow(unit, exp) * (unit - 0.05));
if (exp < 6 && absBytes >= th - ((th & 0xfff) == 0xd00 ? 52 : 0)) exp++;
String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp - 1) + (si ? "" : "i");
if (exp > 4) {
bytes /= unit;
exp -= 1;
}
return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre);
}
Zauważ, że od samego początku chodziło o uniknięcie pętli i nadmiernego rozgałęziania. Kod jest jeszcze mniej czytelny niż wersja pierwotna. Osobiście nie skopiowałbym tego fragmentu kodu do kodu produkcyjnego.
Aby uzyskać zaktualizowany kod o jakości produkcyjnej, zobacz osobny artykuł: Formatting byte size to human readable format.
Kluczowe wnioski
- Fragmenty kodu Stack Overflow, mimo tysiąca pozytywnych opinii, mogą okazać się błędne,
- Przetestuj wszystkie przypadki brzegowe, szczególnie dla kodu skopiowanego ze Stack Overflow,
- Arytmetyka zmiennoprzecinkowa jest trudna,
- Podczas kopiowania kodu należy uwzględnić prawidłowe przypisanie. Ktoś później może zechcieć to zweryfikować.
Artykuł opublikowaliśmy za zgodą autora. Autorem tłumaczenia jest Adam Zamczała. Zdjęcie główne tekstu pochodzi z unsplash.com.
Podobne artykuły

Technologia, która otwiera sklepy. Jak HelpDesk Silky Coders wspiera ekspansję Sinsay?

Oto najlepiej płatne technologie 2025 roku. Sprawdzamy, gdzie najwięcej się zarabia w IT

Najnowsze trendy w IT: co czeka programistów w 2026 roku?
Rynek IT w Polsce 2025: Stabilizacja i koniec kryzysu? [RAPORT]

Data wyprzedza JavaScript – nowy lider polskiego rynku IT w 2025

Consulting technologiczny: 4 mity vs. butikowa rzeczywistość

Świat agentów: automatyzacja i co dalej