Programowanie „przepisu” na rozwiązanie. O algorytmach genetycznych

Obecne branże muszą opracowywać produkty wysokiej jakości w krótkim czasie, ze względu na wymagania dotyczące konkurencji lub cyklu projektowego. Tradycyjne procesy projektowania można znacznie ulepszyć, stosując narzędzia inżynierii obliczeniowej. W miarę rozwoju nowoczesnych technologii obliczeniowych i modelowania, projektowanie inżynierskie w dużym stopniu opiera się na modelowaniu komputerowym i symulacji. Jednak nawet przy pomocy modelowania obliczeniowego proces projektowania jest długą i żmudną procedurą.

Łukasz Rzegociński. Software Architect w Bosch Polska. Ukończył Cybernetykę na WAT i Lotnictwo i Kosmonautykę na Politechnice Warszawskiej. Inżynier sercem, specjalista IT umysłem. Na co dzień tworzy oprogramowanie implementujące wiedzę inżynierską, elementy sztucznej inteligencji służące do automatyzacji procesów konfiguracji produktu i wsparcia procesów projektowania. W ramach R&D szuka rozwiązań na niemożliwe. W międzyczasie po prostu człowiek od rozwiązywania problemów.

Proces ten wymaga wielu eksperymentów i symulacji w celu zbadania koncepcji projektowania. Temat poprawy efektywności jest nadal jednym z głównych wyzwań w dzisiejszym świecie przemysłowym. Dlatego opisuję wykorzystanie algorytmów genetycznych (GA), które są popularnym rodzajem algorytmów wyszukiwania. GA używają idei ewolucji i przetrwania najsilniejszych, aby przeprowadzić wyszukiwanie populacyjne.

W artykule zaproponowałem wykorzystanie algorytmu genetycznego w procesie projektowania produktu, jakim jest czujnik poziomu paliwa w zbiorniku. Przedstawiony został zarys implementacji nowego narzędzia jako rozszerzenia do systemu modelowania komputerowego. Opisane zostały praktyczne wnioski, rezultaty, napotkane problemy.

Projektowanie inżynierskie jako zagadnienie optymalizacyjne

Inżynierowie często stają przed wyzwaniem polegającym na znalezieniu kompromisu pomiędzy różnymi czynnikami w celu osiągnięcia pożądanych rezultatów. A proces znalezienia najlepszego kompromisu nazywamy optymalizacją.

Wiele problemów inżynierskich można zdefiniować jako zagadnienia optymalizacji, np. zautomatyzowane projektowanie komponentów, rozmieszczanie ścieżek drukowanych płytek pcb, harmonogramowanie czy logistyka.

Rozwiązania takich problemów zazwyczaj są trudne do osiągnięcia, ponieważ posiadają rozległe przestrzenie poszukiwań. Trudności dokłada też fakt, że niemożliwe jest znalezienie rozwiązania poprzez próbkowanie każdego punktu w przestrzeni poszukiwań w rozsądnie dopuszczalnym czasie obliczeniowym.

Zmienne czynniki powodują, że trudno jest zdefiniować drogę wprost prowadzącą do rozwiązania. Przy czym rozwiązań może być kilka i każde z nich może być dobre pod kątem innego kryterium.

Słabość technik deterministycznych w przypadku złożonych problemów

Wiemy, że tradycyjne metody deterministyczne wyszukiwania optymalnego rozwiązania nie sprawdzają się w przypadku złożonych problemów inżynierskich.

W praktyce inżynier, analityk, czy manager chcą wynik dający możliwość podjęcia decyzji najszybciej jak się da. Ponadto w przypadku złożonych zagadnień, interesujące jest również poznanie innych rozwiązań bliskich do optymalnego. Może się okazać, że są one tylko nieznacznie gorsze, ale za to dużo łatwiejsze do adaptacji lub wdrożenia i osiągalne dużo szybciej.

Dobrym przykładem jest projektowanie płytek drukowanych układów elektronicznych. Jest wiele rozwiązań spełniających wymagania odnośnie połączenia ścieżek. Ale jeśli spojrzymy od strony procesu wytwarzania i czasu potrzebnego na rozmieszczenie elementów na płytce, to zagadnienie jest tożsame z problemem komiwojażera. Próba rozwiązania tego metodami deterministycznymi wymaga dużej mocy obliczeniowej i nakładu czasu. Metody te w przypadku trudnych do rozwiązania zagadnień, sprawiają również dużo kłopotu w implementacji.

W środowisku gdzie głównym celem jest osiąganie pożądanych wyników finansowych, możemy zaobserwować tendencje do poszukiwania rozwiązania wystarczająco dobrego i możliwego do uzyskania w rozsądnym czasie

Stochastyczne metody optymalizacji, wprowadzenie, wyjaśnienie zasadności zastosowania

“Jeżeli nie możemy podejść wprost do złożonych problemów, to może spróbujmy je chociaż opisać.” Taki cel przyświeca właśnie optymalizacji stochastycznej. Polega ona na optymalizacji rozwiązania, w którym nie jest znany z góry związek funkcjonalny pomiędzy niezależnymi zmiennymi wejściowymi a wynikiem – funkcją dopasowania.

Techniki stochastyczne odgrywają coraz większą rolę w kontroli i analizie współczesnych systemów, jako dostarczające algorytmów stosunkowo niewrażliwych na błędy i nieprzewidywalność ich modelowania, oraz jako sposób radzenia sobie z nieodłącznym szumem systemu.

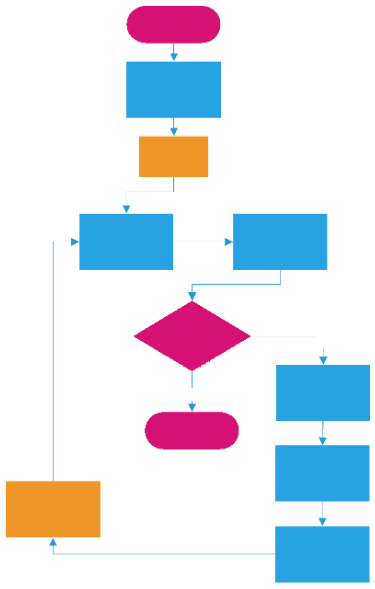
Generalna forma opracowania rozwiązań za pomocą stochastycznej techniki optymalizacji ma postać zgodną z algorytmem na rysunku 3.1.

Opiera się na stworzeniu początkowej puli potencjalnych rozwiązań. Każde z nich jest oceniane pod kątem spełnienia funkcji dopasowania. Na podstawie oceny tworzony jest podzbiór najlepszych rozwiązań. Na podstawie tego zbioru oraz cech najlepszych rozwiązań, tworzony jest kolejny zbiór, będący pulą początkową kolejnej iteracji.

Rys. 3.1 Generalny algorytm optymalizacji stochastycznej

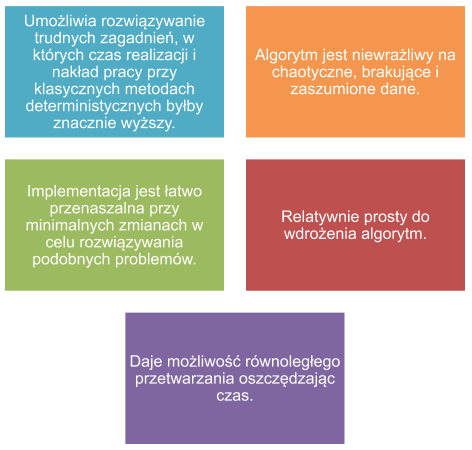
Korzyści optymalizacji stochastycznej:

Algorytm genetyczny (GA) jak metoda znajdowania i optymalizacji rozwiązania

„Spójrz głęboko w naturę, a wtedy wszystko zrozumiesz lepiej.” To słowa Alberta Einsteina, które idealnie streszczają moje poniższe wyjaśnienie.

Algorytm genetyczny (GA) to metoda wyszukiwania i optymalizacji, która funkcjonuje naśladując zasady ewolucji i przetwarzania chromosomów w genetyce. Rozpoczyna ona wyszukiwanie od losowego zbioru rozwiązań. Zbiór ten najczęściej składa się ze zmiennych, losowych obiektów. Każde z rozwiązań ma przypisany wynik, który jest bezpośrednio związany z funkcją przystosowania i wprost określa, jak konkretne rozwiązanie ją spełnia.

Następnie zbiór rozwiązań tzw. “populacja” jest modyfikowany do nowej generacji z zastosowaniem operatorów genetycznych: reprodukcji, krzyżowaniem i mutacją. Algorytm działa iteracyjnie tworząc nowe pokolenie, aż do spełnienia kryterium zakończenia.

Podejście to idealnie sprawdza się w obliczu złożonych problemów inżynierskich. Główną jego zaletą jest elastyczność, która daje możliwość zastosowania go do złożonych zagadnień. Kolejną zaletą jest możliwość holistycznego spojrzenia na problem. W wielu rozwiązaniach klasycznych brak globalnej perspektywy sprawia, że znajdowane rozwiązanie jest optymalne tylko lokalnie. Klasyczne algorytmy są również trudne do zrównoleglenia, wiele obliczeń ma charakter szeregowy.

Algorytmy genetyczne należą do grupy bezpośrednich algorytmów optymalizacji i przeszukiwania. W metodach tych do znalezienia optimum globalnego wykorzystywane są tylko funkcja dopasowania i warunki brzegowe. Ich główną zaletą jest możliwość pracy na nieciągłej domenie i funkcji dopasowania (np. problem komiwojażera), możliwość zrównoleglenia oraz elastyczność w zastosowaniu do różnych problemów. Wadą metod bezpośrednich jest ich powolność, oraz czułość na losowość populacji startowej.

Wprowadzenie, nawiązanie do procesu ewolucji w naturze

Idea algorytmów genetycznych bazuje na zasadzie ewolucji sformułowanej przez Darwina. Natura w większości przypadków stosuje dwie fundamentalne zasady: po pierwsze jeżeli w wyniku przetwarzania genetycznego powstanie potomstwo o ponadprzeciętnych parametrach, zwykle przetrwa ono dłużej i posiada większą szansę na wyhodowanie dzieci i o lepszych cechach niż przeciętny osobnik. Z kolei potomstwo o parametrach poniżej średniej zwykle nie przeżyje dłużej, dlatego też zostanie wyeliminowane z populacji.

Co różni algorytm genetyczny od natury to, to że mamy bezpośredni wpływ na funkcje ewolucji. Jest ona implementowana bezpośrednio pod kątem uzyskania konkretnego rezultatu. W istocie algorytm genetyczny nie jest tak złożony jak naturalna selekcja i genetyka, a jest raczej abstrakcją naturalnego procesu ewolucyjnego.

Zasada działania (populacja, funkcja dopasowania, reprodukcja, krzyżowanie, mutacje)

Realizacja algorytmu GA polega na iteracyjnym przetwarzaniu populacji aż do spełnienia kryterium zakończenia, które określa poziom satysfakcjonującego nas rozwiązania. Dopóki kryterium końcowe nie jest spełnione kolejne populacje są modyfikowane przy użyciu trzech różnych operatorów: reprodukcja, krzyżowanie, mutacja.

Reprezentacja rozwiązania w GA jest podobna do naturalnego chromosomu, a operatory GA podobne do operatorów genetycznych.

Populacja początkowa może zostać ograniczona warunkami brzegowymi, jeżeli są możliwe do zdefiniowania. Jej zawężenie poprawia czas uzyskania zbieżności. Efektem ubocznym może być fakt, że znajdziemy tylko optimum lokalne.

W przypadku, gdy nie mamy wiedzy na temat dziedziny problemu możemy rozpocząć wyszukiwanie od losowej populacji rozwiązań.

Nawiązując do przykładu z płytką drukowaną, przykładową populacją startową będą zbiory (chromosomy) opisujące różną kolejność montowania elementów na płytce.

Dla każdego rozwiązania z populacji w każdej iteracji wyznaczany jest wynik funkcji dopasowania. Ocenia on dopasowanie rozwiązania do kryteriów zawartych w funkcji dopasowania. Lepsze dopasowanie to wyższy wynik, większa szansa na przetrwanie.

Funkcja przystosowania razem z kryteriami brzegowymi definiuje w jakim kierunku ewoluuje rozwiązanie. To w niej obok warunków brzegowych populacji znajdują się reguły definiujące problem.

Pomiędzy iteracjami kolejne generacje przygotowane są w wykorzystaniem operatorów genetycznych.

Powielanie (lub selekcja) jest zwykle pierwszym operatorem stosowanym przy budowaniu populacji kolejnej generacji. Powielanie wybiera najlepsze rozwiązania (chromosomy) i powiela je. Ilość powieleń może być uwarunkowana od wartości funkcji przystosowania konkretnego chromosomu. Wielkość populacji zwykle utrzymywana jest na tym samym poziomie.

Krzyżowanie polega na losowym wybraniu dwóch rozwiązań (chromosomów) i częściowej wymiany pomiędzy nimi genów. Operator ten jest głównie odpowiedzialny za możliwość wykorzystania GA do wyszukiwania.

Operator mutacji odpowiada przede wszystkim za utrzymanie różnorodności populacji. Jego działanie polega na losowej zmianie genu lub genów w chromosomie. Taka losowość jest przydatna szczególnie w celu poprawy lokalnego optimum.

Działanie wszystkich tych trzech operatorów jest jednoznaczne.

Żadne z działań operatorów nie jest gwarantowane i nie jest testowane podczas tworzenia nowej populacji rozwiązań. Mechanizm działania sprawia, że nawet jeśli w drodze zastosowania operatorów powstaną gorsze rozwiązania, zostaną one wyeliminowane przez operator powielania w następnej w populacji.

Rys. 4.1 Zasada działania algorytmu genetycznego

Przykład zastosowania w praktyce – projektowanie ramienia pływaka poziomu paliwa w samochodzie

Poniżej zobaczycie praktyczne zastosowanie metody optymalizacji z użyciem GA do rozwiązania zadania inżynierskiego. Polega ono na znalezieniu geometrii drucianego ramienia pływaka w czujniki poziomu paliwa.

Aktualny proces składa się w wielu powtarzalnych kroków, w których inżynier z pomocą systemu CAD projektuję geometrię ramienia pływaka. Jest ona zależna od kształtu zbiornika paliwa, wymaganych do zmierzenia poziomów paliwa czy rodzaju paliwa.

Kształt zbiornika paliwa ulega częstym zmianom podczas projektowania samochodu, ponieważ zazwyczaj jest komponentem, który wypełnia możliwe wolne przestrzenie. Wynika to z jego wielkości i umiejscowienia.

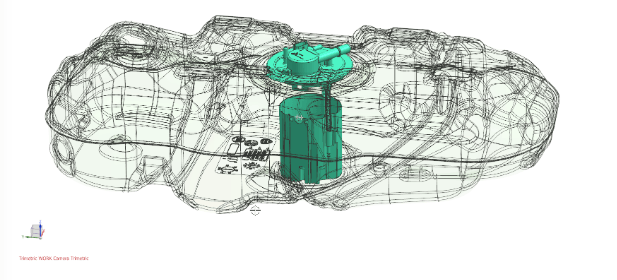
Rys. 5.1 Geometria wejściowa – zbiornik paliwa wraz z obudową pompy paliwa

Każda taka zmiana wymusza ponowne przeliczenie i sprawdzenie czujnika mierzącego poziom paliwa. Powtarzalność tych obliczeń oraz standaryzacja procesu projektowania daje duży potencjał do automatyzacji.

Opisanie problemu od strony inżynierskiej

Problem wyznaczania geometrii czujnika poziomu paliwa jest przykładem optymalizacji wielo-parametrycznej. Przestrzenią poszukiwania rozwiązania jest cała objętość zbiornika paliwa. Ograniczeniami wpływającymi na potencjalne rozwiązania są wymagane do zmierzenia poziomy paliwa, standaryzacja niektórych komponentów, z których zbudowany jest czujnik, ograniczenia związane z procesem wytwarzania drucianego ramienia, mechaniczne opory ruchu ramienia.

Optymalizacja jest prowadzona w kierunku znalezienia rozwiązania spełniającego wszystkie warunki brzegowe oraz o najniższym koszcie wytworzenia. W tym przypadku zależy nam na zużyciu najmniejszej ilości drutu oraz najmniejszej ilości punktów gięcia.

Ogólny zarys implementacji, użyte technologie

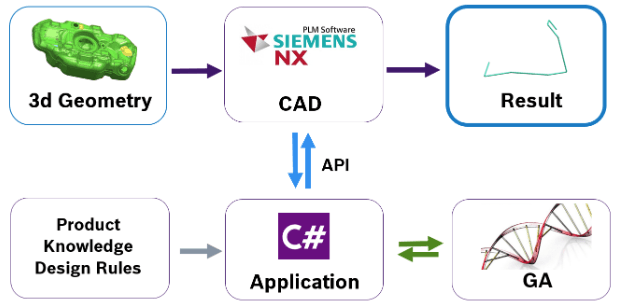
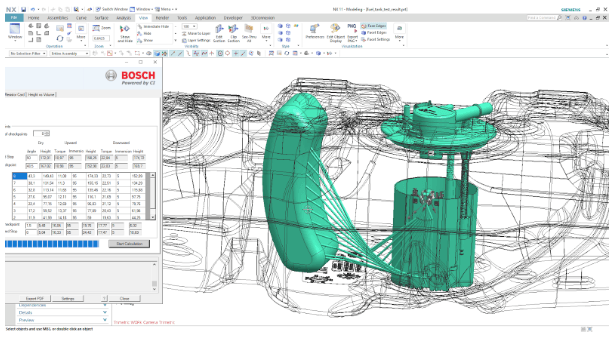
Aplikacja została zrealizowana jako rozszerzenie do systemu CAD Siemens NX. Było to podyktowane koniecznością interakcji z geometrią 3d zbiornika paliwa, ponadto wynikiem optymalizacji jest model 3d pływaka wraz z rysunkami wykonawczymi. Komunikacja aplikacji z systemem CAD wykorzystująca API NXOpen C#.

Na rynku istnieje wiele gotowych rozwiązań implementujących metody optymalizacji z użyciem GA. Biblioteki te dają możliwość elastycznego definiowania przestrzeni poszukiwań (populacji), funkcji dopasowania, czy operatorów genetycznych. Dlatego też w przedstawianej realizacji zdecydowano się wykorzystać gotową bibliotekę, a główny ciężar implementacji położyć na wydajną integrację z systemem CAD.

Rys. 5.2 Jak to działa

Gen został zdefiniowany jako pojedynczy punkt 3d w przestrzeni wewnątrz zbiornika paliwa. Chromosom stanowiący zbiór genów, opisuje pojedynczą możliwą geometrię ramienia pływaka. Każdy z genów może opisywać pozycje końcowa, początkową, lub punkt gięcia drutu.

Podczas ewaluacji poszczególnych chromosomów funkcja przystosowania ocenia jak dobrze losowa kombinacja genów spełnia kryteria odnośnie reguł projektowych, ograniczeń wytwarzania, czy wymagań odnośnie mierzonych poziomów paliwa.

Funkcja przystosowania mierzy jakość aktualnego rozwiązania. To w niej znajdują się reguły opisujące rozwiązanie, co stanowi ok. 90% całej implementacji. Z tego też względu ważne jest żeby była napisana wydajnie.

Spośród całej populacji wybieramy 30% najlepszych rozwiązań i na ich podstawie z wykorzystaniem operatorów genetycznych tworzymy kolejna generacje.

Po około 25 iteracjach aplikacja oferuje już wystarczająco dobre rozwiązanie, spełniające wszystkie wymagane kryteria z określoną dokładnością. Zwiększenie liczby iteracji powoduje wydłużenie czasu obliczeń, a nie przynosi dużej poprawy w wyniku.

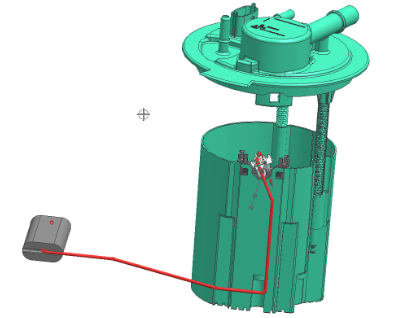
Dla najlepszego rozwiązania tworzony jest model 3d ramienia i oraz wizualizacja jego ruchu wewnątrz zbiornika paliwa.

Rys. 5.3 Rezultat pracy aplikacji, ramię pływaka wraz z symulacją ruchu.

Napotkane problemy

Głównym problemem, który przewijał się podczas implementacji, była proporcja czasu potrzebnego na obliczenia do jakość otrzymanego rozwiązania.

Przyjęte od początku założenie pracy w interfejsie użytkownika systemu CAD niosło ze sobą pewne ograniczenia, jak i korzyści. Korzyścią jest łatwość prowadzenia interakcji pomiędzy użytkownikiem a aplikacją, oraz podgląd rezultatu na żywo. Ograniczeniem natomiast był brak możliwości zrównoleglenia obliczeń. Wynika to z faktu ograniczenia systemu CAD, w którym to dużej części operacji nie można wykonywać równolegle. Możliwe jest uruchomienie kilku sesji systemu CAD, ale rozwiązanie takie porzucono ze względu na ograniczone zasoby sprzętowe komputera użytkownika, oraz znaczne podniesienie stopnia komplikacji całego rozwiązania. Koszt implementacji przysłaniał zysk ze zrównoleglenia.

Możemy ponadto wskazać dwa główne czynniki wpływające na czas obliczeń. Przede wszystkim czas wykonywania operacji po stronie systemu CAD oraz stopień dyskretyzacji przestrzeni 3d. Każde przeliczenie po stronie systemu CAD czy to odległości pomiędzy obiektami, czy też ich wzajemnego przenikania zajmuje kilkanaście milisekund.

W sytuacji, gdy takie operacje wykonujemy setki tysięcy razy, zaczyna mieć to znaczenie. W efekcie pierwszy prototyp aplikacji potrzebował kilku godzin na znalezienia dość dobrego rozwiązania. Celem było kilka – kilkanaście minut. Aby to osiągnąć, interakcja z systemem CAD została sprowadzona do minimum. Większość obliczeń geometrycznych odbywa się w formie matematycznej po stronie aplikacji.

Celem zmniejszenia czasu obliczeń aplikacja analizuje również wymagania użytkownika i geometrie zbiornika jeszcze przed stworzeniem początkowej populacji, celem pominięcia w zbiorniku obszarów, które już na wstępie nie rokują na dobre rozwiązanie.

Istotne jest jak najbardziej losowe rozmieszczenie punktów populacji początkowej wewnątrz zbiornika paliwa. Pozwala to kosztem mniejszej ilości iteracji uzyskać wystarczająco dobry wynik.

Rezultaty

Już podczas pierwszych testów aplikacja była w stanie „zadziwić” inżynierów, dając rozwiązanie, o którym nigdy by nie pomyśleli, a które było dobre i spełniało wszystkie wymagane kryteria.

Rys. 5.4 Zaprojektowane przez aplikacje ramię pływaka

Przedstawione rozwiązanie jest idealnym przykładem ukazującym skuteczność metody optymalizacji z użyciem GA do rozwiązywania złożonych problemów inżynierskich.

Aplikacja implementuje w sobie wiedzę inżynierską z zakresu projektowania i wytwarzania ramienia pływaka. Z jednej strony daje korzyść w postaci automatyzacji i zwolnienia zasobów ludzkich z monotonnych i powtarzalnych zadań w kierunku bardziej kreatywnej pracy. Zabezpieczając z drugiej strony jakość i czas dostarczenia rozwiązania.

W zależności od parametrów wejściowych aplikacja potrzebuje ok 15-25 min na znalezienie i zaprezentowanie rozwiązania. W przypadku manualnej pracy, doświadczony inżynier potrzebował ok. 8h pracy. Oszczędność czasu jest zatem znaczna.

Korzyści i ograniczenia optymalizacji z użyciem GA

Największą zaletą jest jej elastyczność i łatwość stosowania w przypadku złożonych problemów. W przypadku metod optymalizacji GA nie staramy się bezpośrednio zaimplementować rozwiązania. Patrzymy holistycznie i implementujemy opis dobrego rozwiązania najlepiej jak to się da. Resztę zostawiamy ewolucji.

Metoda optymalizacji GA opiera się na pomiarze jakości danego rozwiązania. Coś co jest z jednej strony korzyścią, jest również ograniczeniem. Nigdy nie mamy gwarancji czy uzyskany z optymalizacji wynik jest najlepszy. Jest dość dobry, aby spełnić założone kryteria i tylko tego możemy być pewni. Dla takich samych warunków wejściowych zwykle otrzymamy inny rezultat. Z tego wynika zatem, że aby otrzymać statystycznie zbieżny wynik, należy przeprowadzić kilka symulacji. A to z kolei podnosi czas trwania obliczeń.

Jakość otrzymanego rozwiązania również maleje wraz ze wzrostem złożoności implementowanego problemu.

Metoda ta jest również wrażliwa na jakość początkowej populacji. Musimy zapewnić jak największą możliwą losowość podczas tworzenia początkowych rozwiązań.

Podsumowanie

Opisany powyżej problem inżynierski byłby bardzo trudny lub wręcz niemożliwy do implementacji klasycznymi technikami deterministycznymi. W przypadku algorytmu genetycznego było to możliwe, ponieważ skupiamy się programowaniu „przepisu” na rozwiązanie, niż bezpośrednio samego rozwiązania.

Optymalizacja z użyciem algorytmów genetycznych zyskuje coraz większą popularność przede wszystkim na uniwersalność zastosowania, możliwość zrównoleglenia, oraz globalna perspektywę.

Elastyczność GA w rozwiązywaniu problemów związanych z wyszukiwaniem i optymalizacją, takich jak optymalizacja wielokryterialna, jest głównym powodem wzrostu ich popularności w rozwiązywaniu różnych problemów inżynierskich.

Zdjęcie główne artykułu pochodzi z unsplash.com.

Oferty pracy z