Sieci neuronowe. PyTorch i praktyczny projekt od początku do końca

W poniższym artykule postaram się przedstawić podstawy wiedzy niezbędne do budowy pierwszego modelu głębokiego sieci neuronowej. W ramach tego zadania będę próbował zredukować przerażającą na pierwszy rzut oka stronę matematyczną i skupię się na praktycznym wykorzystaniu jednego z wielu dostępnych narzędzi. Wśród nich: biblioteka PyTorch, która w zakresie pomocy uporania się z treningiem sieci oraz jego walidacją sprawdza się znakomicie.

Spróbujemy określić ramy objęte przez samą bibliotekę, następnie poruszymy podstawowe pojęcia matematyczne związane z uczeniem maszynowym, a wisienką na torcie będzie przykład budowy modelu klasyfikatora XOR, który będzie przewidywał z prawie stuprocentowym prawdopodobieństwem wynik operacji XOR liczb zmiennoprzecinkowych. Tym dość prostym przykładem mam nadzieję przedstawić istotę istnienia szeroko pojętej sztucznej inteligencji. Zatem zaczynamy!

O bibliotece PyTorch słów kilka…

PyTorch jest otwartą biblioteką (otwartość biblioteki oznacza, iż każdy może być kontrybutorem, czyli współtwórcą rozwiązań – kod jest dostępny dosłownie dla każdego) stosowaną w obszarze uczenia maszynowego do tworzenia głównie pełnych rozwiązań mających za zadanie finalnie dostarczyć model sieci neuronowej rozwiązującej dany problem.

Nazwa biblioteki pochodzi od zestawienia dwóch terminów – „Python” (obecnie główny język programowania, dla którego rozwijana jest biblioteka) oraz „Torch”, czyli dawniej biblioteki, która została napisana w języku „Lua” – języku, który powstał w latach 90. w Brazylii i znany był z łatwości integracji z innymi językami oraz stosunkowo łatwej możliwości optymalizacji kodu pod względem szybkości działania.

Torch jest popularną biblioteką rozwijaną głównie przez zespoły badawcze z obszaru nauczania maszynowego. PyTorch jest właśnie próbą rozszerzenia biblioteki Torch na język Python, obudowaną w dodatkowe funkcjonalności wynikające z samego środowiska tego języka. W tym miejscu zakładam, iż posiadasz wszelkie zależności potrzebne do pracy z językiem Python – jeśli nie, proponuję zacząć od instalacji, która została świetnie opisana na oficjalnej stronie.

Fundamentem obliczeniowym biblioteki PyTorch stała się inna biblioteka numeryczna – numpy. Można dla uproszczenia stwierdzić, iż PyTorch znacząco rozszerzył działanie nadmienionej biblioteki na potrzeby obliczeń stosowanych w nauczaniu maszynowym. Główne usprawnienia, jakie wprowadził PyTorch to możliwość procedowania skomplikowanych obliczeń na tensorach (czyli odpowiedniku tablic, z ang. array) przy użyciu GPU (graficznej jednostki obliczeniowej, a dokładniej — procesora karty graficznej).

Przeznaczeniem GPU jest wykonywanie skomplikowanych obliczeń na rzecz szeroko pojętej grafiki komputerowej. Arytmetyka stojąca za operacjami transformacji układów współrzędnych w odniesieniu do manipulacji obiektów w przestrzeni trójwymiarowej jest dość skomplikowana, a dla zadowalających efektów wizualnych obliczenia te muszą być wykonane niezwykle szybko. To z kolei zapewnia architektura procesorów graficznych, które przetwarzają równolegle duże zadania dzieląc je na mniejsze podzadania. Ze względu na efektywność pracy GPU świetnie nadaje się do obliczeniowo wymagających zadań związanych z uczeniem głębokim – obliczenia z reguły są wykonywane ponad 50 razy szybciej przy użyciu powszechnie stosowanych kart graficznych.

Instalacja biblioteki PyTorch

Aby zainstalować wszystkie zależności potrzebne do użycia biblioteki PyTorch, warto wykorzystać do tego celu narzędzie pip, czyli pakiet służący do instalacji zależności (czyli na przykład zewnętrznych bibliotek, artefaktów). Jeśli jeszcze nie posiadasz pakietu pip, możesz przeczytać o jego instalacji na oficjalnej stronie.

Oczywiście nie jest to jedyny sposób instalacji biblioteki PyTorch – więcej możesz przeczytać na oficjalnej stronie pakietu.

Kolejną kwestią jest środowisko, w którym zaczniemy pisać dany kod – nie wpływa ono na możliwość wykonania napisanego programu. Zachęcam jednak do stosowania i uczenia się od początku wiodących środowisk programistycznych (ang. IDE, czyli Integrated Development Environment). Integracja dotyczy wielu zasobów oraz rozszerzeń, które znacznie ułatwiają pracę, automatycznie poprawiają błędy składniowe, sugerują zmiany celem osiągnięcia przejrzystego kodu, co znacznie usprawnia pracę i pozwala cieszyć się działającym programem nawet za pierwszym razem!

W tym przykładzie będę stosował darmowe środowisko Visual Studio Code, lecz polecam również spróbowanie innych środowisk takich jak na przykład Fleet produkcji JetBrains.

Oferty pracy z

Tensory, czyli podstawa obliczeniowa biblioteki PyTorch

Zacznijmy zatem od podstaw. W utworzonym w dowolnej, wygodnej dla Ciebie lokalizacji stwórzmy plik DL_training.py. W wybranym pliku rozpoczniemy naszą naukę podstaw. Aby zacząć używać biblioteki PyTorch, w swoim rozwiązaniu musimy zaimportować zainstalowany wcześniej pakiet (przy instalacji biblioteki PyTorch). W tym celu na początku naszego pliku definiujemy sekcję importowania używanych pakietów:

Głównym obiektem matematycznym uwzględnianym w obliczeniach jest tensor. Jest on pojęciem ściśle matematycznym, w dużym uproszczeniu możemy przyjąć, że jest to uogólnienie macierzy (czyli dwuwymiarowego tensora) na przestrzeń wielowymiarową, natomiast w przypadku biblioteki PyTorch jest mocnym nawiązaniem do królowej nauk. Tensor w tym przypadku jest po prostu obiektem klasy, która w bardzo efektywny sposób odzwierciedla arytmetykę tensorową.

W dodatku posiada wiele innych zalet poprzez bardzo przejrzyste API – wśród nich jest na przykład możliwość transponowania tensora, rozkładu Choleskiego (umożliwia on jednolinijkowym wywołaniem znaleźć tensor, który pomnożony przez swoją transponowaną postać da właśnie tensor pierwotny, na którym operujemy) i wiele więcej. Ale nie zamierzam dalej straszyć, bo w rzeczywistości omawiana biblioteka pozwala nam zapomnieć o większości operacji, które śnią się studentom po nocach.

Wszystkie funkcjonalności tej klasy możecie sprawdzić, czytając oficjalną dokumentację. Chcąc stworzyć tensor o wymiarach 3x3x3 (co zwizualizować możemy kostką Rubika 3x3x3) piszemy następującą linię kodu:

W efekcie uzyskujemy następujący tensor:

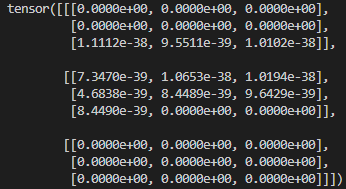
Jeśli dobrze się przyjrzysz, zauważysz wewnątrz trzy macierze (lub tablicę, jak kto woli), które zawierają po 3 rzędy oraz 3 kolumny. Klasa Tensor umożliwia wykonywanie wielu operacji, z pewnością większość potrzebnych do codziennej pracy w obszarze nauczania głębokiego jest gotowa do użycia. Zapewne padnie pytanie, po co w ogóle opisuję tę klasę? Otóż bardzo ważną częścią całego procesu treningu sieci jest prawidłowe przygotowanie danych, na których będziemy ową sieć trenować oraz walidować uzyskane potreningowe wyniki. Obróbka danych wiąże się często z wieloma operacjami manipulacji danymi zawartymi w wielowymiarowych tablicach.

Proste, a zarazem wyjątkowe – czyli o gradiencie, pochodnej i dynamicznej kreacji grafu słów kilka

Omówmy teraz zatem jedno z zagadnień, które znacząco wyróżnia PyTorch na tle biblioteki numpy. Otóż PyTorch świetnie nadaje się do zastosowań w obszarze tworzenia środowisk uczenia maszynowego ze względu na to, iż w bardzo prosty i szybki sposób możemy uzyskać dostęp do obliczeń gradientu oraz pochodnych funkcji, na których operujemy (a operujemy na danych liczbowych, natomiast relacje pomiędzy kolejnymi warstwami sieci są ściśle określone poprzez konkretne równania).

W prosty sposób możemy przyjąć, iż o pochodnej będziemy myśleć w przypadku, gdy nasza sieć będzie posiadać jedno wyjście (które na przykład będzie określało prawdopodobieństwo zdarzenia, że zaprezentowane sieci zdjęcie przedstawia wybrane zwierzę). W przypadku wielu wyjść będziemy używać pojęcia gradientu. Zarówno gradient, jak i pochodna określa tempo oraz trend zachowania danej funkcji względem danej zmiennej lub zmiennych. Po co nam wymienione mechanizmy? O tym za chwilę poniżej. Dodatkowo, w przypadku omawianej biblioteki często wspomina się o niezwykle ważnym pojęciu – dynamicznej kreacji grafu, który prezentuje trend i tempo zmian finalnego wyniku (wyjścia naszego układu) w zależności od danego wejścia w tym układzie.

Przejdźmy zatem do przykładu, na podstawie którego postaram się pokazać, jak możemy rozumieć formułę i rolę określania za pomocą pochodnej funkcji (lub gradientu) tempa i trendu zmiany funkcji (czyli faktu, czy rośnie w danym punkcie, czy maleje). Gdybyśmy mogli w jakiś sposób zdefiniować funkcję, która opisywałaby, jak zmieni się nasz nastrój w zależności od temperatury, mogłaby ona wyglądać tak:

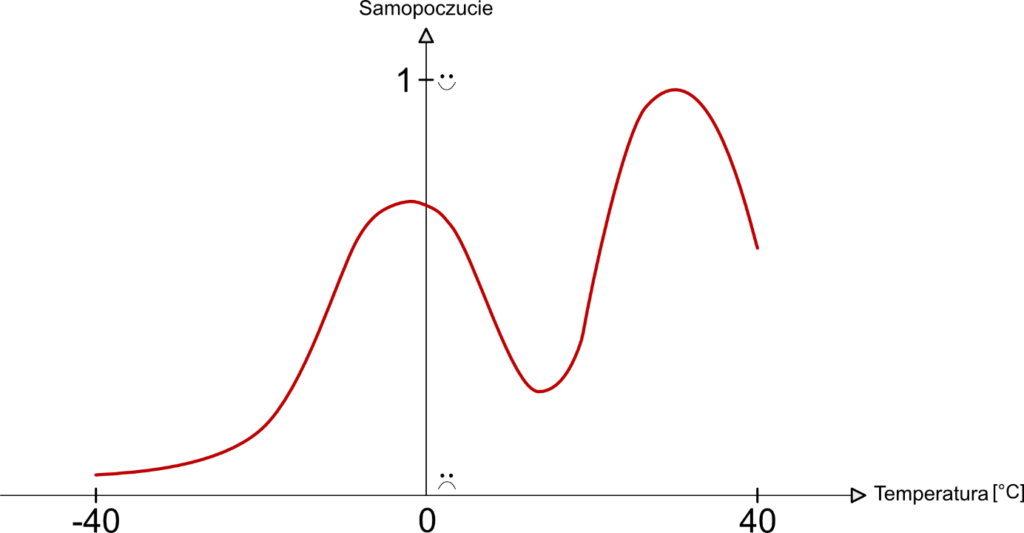
W tym przypadku funkcję matematycznie można zapisać następująco:

Chcąc poznać dynamikę danej funkcji, powinniśmy poznać pochodną powyższej funkcji nastroju w zależności od temperatury, czyli zapisując to matematycznie:

Kontynuując wywód i opierając go na przykładzie, dynamika nastroju (czyli pochodna funkcji nastroju po temperaturze) będzie dodatnia dla punktu x1 a ujemna dla punktu x2.

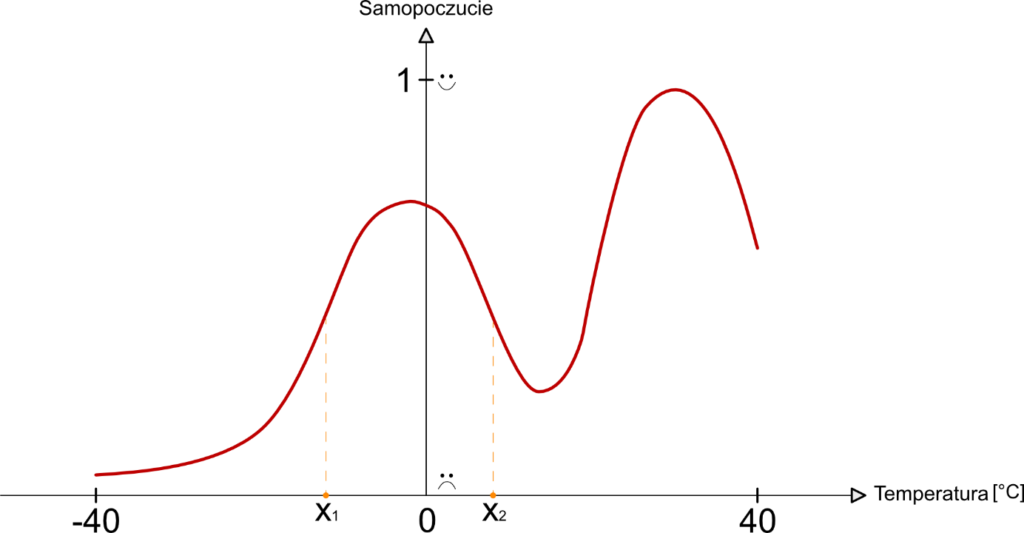
Oczywiście, nawiązując do dynamiki danej funkcji, im większa „stromość” danej funkcji w danym punkcie, tym pochodna ma większą wartość (lub jeśli funkcja w danym punkcie maleje, tym wartość mniejsza lub inaczej – bardziej ujemna). Poznając funkcję pochodnej nastroju od temperatury dowiadujemy się tak naprawdę jak bardzo wrażliwy jest nastrój na temperaturę. To bardzo ważna informacja w kontekście oceny ich relacji, znajdowania temperatury, dla której nastrój ma najwyższą wartość (czyli jest najlepszy), a dla jakiej najgorszy (czyli ma wartość najmniejszą).

Głęboką sieć neuronową możemy również rozpatrywać jako funkcję, która za argumenty wejściowe przyjmuje wiele danych liczbowych (czego uogólnieniem jest tensor wejściowy), a wynikiem zazwyczaj jest również ogólnie rzecz ujmując tensor (czyli jedno lub więcej wyjść). Sieć neuronowa konceptualnie poszukuje wpływu każdego z argumentów wejściowych na wyjście zgodnie z oczekiwaniami (zazwyczaj zgodnie z danymi, które prezentują empiryczną relację argumentów wejściowych na zadane wyjście(a) – na przykład wyników badań krwi na poprawność pracy serca).

Sieć neuronowa nadaje każdemu wejściu wagi, aby w ten sposób móc ważyć wpływ każdego parametru na zadane wyjście. Jednym z głównych zadań algorytmu jest poznanie funkcji wrażliwości (gradient) danych wag wejściowych w odniesieniu do rezultatu, jaki ma ta sieć nam prezentować (a dokładniej, w odniesieniu do funkcji kosztu, czyli błędu pomiędzy oczekiwanym wynikiem a wynikiem sieci). W tej grze chodzi o to, aby poprzez manipulację wagami danych wejść, zminimalizować błąd (pomyłkę) sieci co do rezultatu. Przy dobrze zorganizowanych danych treningowych sieci znamy te rezultaty w odniesieniu do zadanych wejść sieci, dlatego możemy wprost obliczyć, jak bardzo nasz model sieci neuronowej się pomylił.

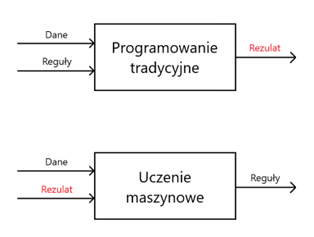
Lubię traktować obszar nauczania maszynowego jako kolejny paradygmat programowania. W celu wyjaśnienia zamieściłem poniższą ilustrację, która ilustruje pewne odwrócenie zależności, gdzie widać, iż algorytmicznie w przypadku uczenia maszynowego staramy się znaleźć reguły (zależności) zachodzące pomiędzy danymi wejściowymi a rezultatami, jakie uzyskujemy. Model, który zna reguły, jest w stanie dla nowych danych wejściowych przewidzieć rezultat zazwyczaj z zadowalającym prawdopodobieństwem.

Podróż przez tajniki implementacji modelu sieci neuronowej na praktycznym przykładzie klasyfikatora XOR

Omówienie rozwiązania oraz implementacja generatora danych treningowych dla sieci

W celu poznania podstawowych komponentów, które pozwolą nam w prosty sposób zbudować model naszej pierwszej sieci, rozpatrzymy przykład sieci, której zadaniem będzie klasyfikacja pary liczb do dwóch grup. Albo grupy, której wynik operacji XOR da 0 lub grupy, której wynik operacji XOR da 1. Dla niewtajemniczonych dodam, iż operacja XOR jest dość prostą operacją. Polega ona na przyjęciu: dwóch liczb (zazwyczaj są to liczby naturalne 0 lub 1) oraz tego, że oczekiwany wynik jest równy zeru, gdy dwie liczby są takie same. Dla par (0,0) i (1,1) otrzymujemy na wyjściu 0, natomiast dla par różniących się (0,1) lub (1,0) otrzymujemy na wyjściu 1.

Problem pojawia się w momencie, gdy założymy, że nasze liczby nie są liczbami całkowitymi, to znaczy jak mamy interpretować parę liczb (0.1,1.3)? W realnym świecie, gdzie operacjami rządzą układy elektroniczne, nie możemy idealnie zakładać, że zawsze otrzymamy idealne liczby na wejściu. Może i jest to dość abstrakcyjny przykład, ale zapewne dostrzegacie, że następuje to zgrzyt pomiędzy teorią a praktyką.

Wyobraźmy sobie, że musimy dokonać operacji XOR dwóch wejść, które podają napięcie z zakresu od 0V do 1.3V. To napięcie prawie zawsze nie będzie idealnie równe liczbie całkowitej, zawsze będzie to „coś po przecinku”. Dla takiego układu musimy stworzyć model, który będzie potrafił sklasyfikować (stąd nazwa sieć klasyfikacyjna lub klasyfikator) daną parę liczb do dwóch grup – albo do grupy par liczb, dających w wyniku operacji XOR 0 lub do grupy par liczb, które w wyniku operacji XOR dadzą 1. W celu wygenerowania losowych danych, na których dokonamy późniejszego treningu (uczenia) naszej sieci, napiszmy nieco kodu definiującego klasę właśnie odpowiedzialną za to zadanie:

Po uruchomieniu naszego program zmienna xor_dataset powinna zawierać tensor (a dokładniej parę określaną jako tuple) dwóch elementów – jeden z nich to kolejny tensor, który zawiera zbiór 300 elementów par losowo wygenerowanych liczb, a drugi element to oczekiwany wynik operacji XOR pary liczb z pierwszego tensora. Oczekiwany wynik jest podawany w sieci, aby ta mogła na bieżąco „dostrajać” wagi w tym przypadku dwóch wejść (na wejściu mamy parę liczb) tak, aby wyjście z jak największym prawdopodobieństwem pokrywało się z tym, czego oczekujemy na podstawie wygenerowanych danych.

Wizualizacja wygenerowanych danych

Chcąc zwizualizować nasze dane możemy użyć pakietu matplotlib, który zawiera wszystko do wygodnego zaprezentowania tego, na czym nam zależy. Oto wynik prezentacji:

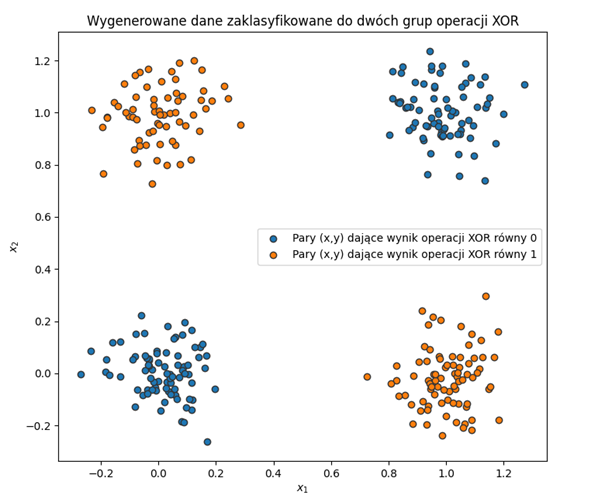
Jak widać, pary liczb, które są różne (zaokrąglają się do różnych liczb całkowitych) i wedle operacji XOR dają wynik 1 (pomarańczowe punkty), znajdują się w lewej górnej oraz prawej dolnej części wykresu, przeciwnie do par, które zaokrąglają się do tych samych wartości. Teraz zajmiemy się próbą zdefiniowania architektury oraz działania naszego modelu głębokiej sieci neuronowej tak, aby ta mogła dla dowolnego punktu danego tej sieci (nawet takiego, którego nie było w danych, na których sieć była uczona) określić, do jakiej grupy należy.

Oczywiście, ten problem jest stosunkowo prosty celem zaprezentowania zwięzłego przykładu, ale każdy problem, który da się opisać liczbowo, może później zostać poddany próbie nauczenia sieci tego, w jaki sposób te dane są powiązane z informacją końcową, która interesuje użytkownika (na przykład wyniki badań krwi z daną jednostką chorobową).

Danie główne, czyli implementacja procesu treningowego naszego modelu sieci neuronowej

Skupimy się teraz na zbudowaniu modelu sieci neuronowej oraz zdefiniowaniu procesu treningu (uczenia) sieci. W tym celu od razu zaprezentuję kod opisujący architekturę sieci, która jest niezwykle prosta.

Pierwszym szczegółem jest użycie modułu torch.nn – skrót „nn” pochodzi od pojęcia neural network. Jest to moduł, który pozwala nam w łatwy sposób zdefiniować strukturę naszego modelu sieci neuronowej. W naszym przypadku, ponieważ jest to dość prosty problem, jest to struktura składająca się z:

• Warstwy wejściowej (wejściowa para liczb),
• Warstwy zwanej ukrytą (wszystkie warstwy głębokich sieci neuronowych poza warstwą wejściową i wyjściową nazywane są zwyczajowo ukrytymi),
• Warstwą wyjściową, która prezentuje już interesujący nas wynik.

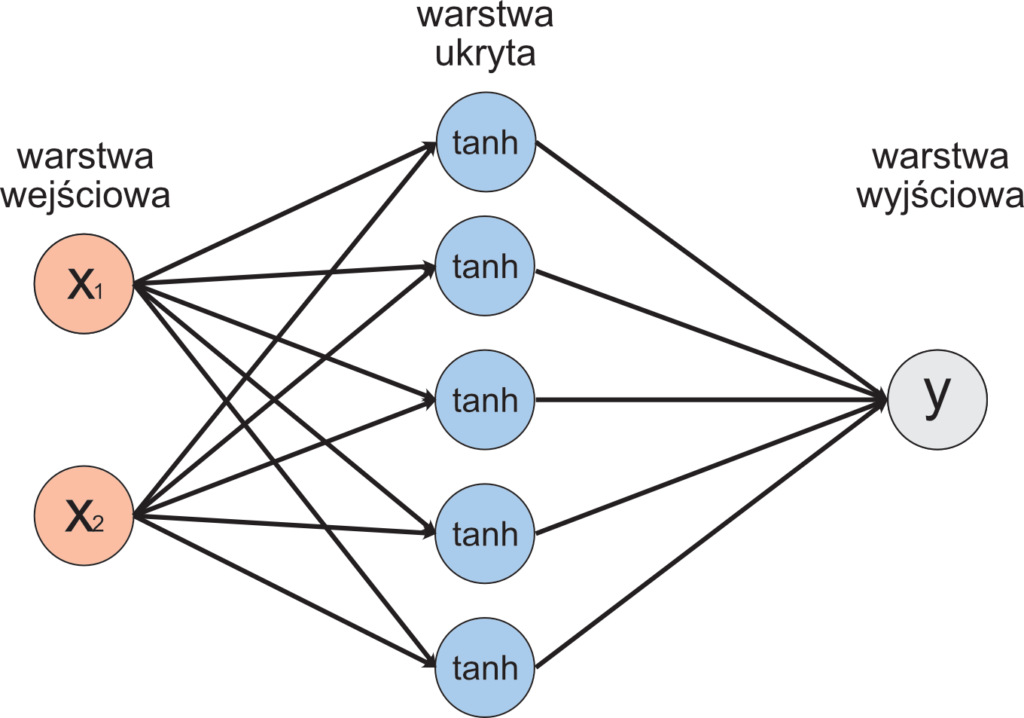
Klasa ClassifierModel definiuje model naszej głębokiej sieci klasyfikatora. W konstruktorze za argumenty wejściowe przyjmujemy ilość neuronów poszczególnych warstw (ilość komórek przyjmujących dane oraz propagujących je dalej w przetworzonej formie). Skupmy się na wyjaśnieniu zdefiniowanych relacji między warstwami – tutaj widać konkretne odwołanie do modułu nn zawierający wiele modeli klas, które pozwalają nam w prosty i przejrzysty sposób zaprojektować naszą sieć. Idąc kolejno po każdej linii naszej klasy, napotykamy na definicję pierwszej transformacji:

Definiujemy tę transformację jako liniową (nn.Linear), czyli taką, która jest standardową definicją wiążącą wejścia, które są ważone (nadawane są im wagi, czyli liczby, przez które są mnożone wejścia, a ustalane są przez sieć w procesie uczenia tak, aby jak najlepiej odzwierciedlać wyuczonym modelem opisaną w danych treningowych przez nas sytuację), a zaprezentowane mogą zostać za pomocą dość prostego wzoru funkcji liniowej:

gdzie:

– macierz wag wejść odpowiadających kolejno każdemu z
neuronów warstwy ukrytej.

Funkcja liniowa poprzez odpowiedni dobór wag w wektorze W stara się zminimalizować błąd (pomyłkę) modelu sieci na podstawie dostarczonych danych treningowych. Opisywany problem jest dość prosty i da się opisać analitycznie w sposób liniowy, natomiast niestety większość musi zostać opisana za pomocą nieliniowych funkcji.

Spójrzmy przy okazji na poniższą ilustrację prezentującą przepływ danych do jednego neuronu warstwy ukrytej:

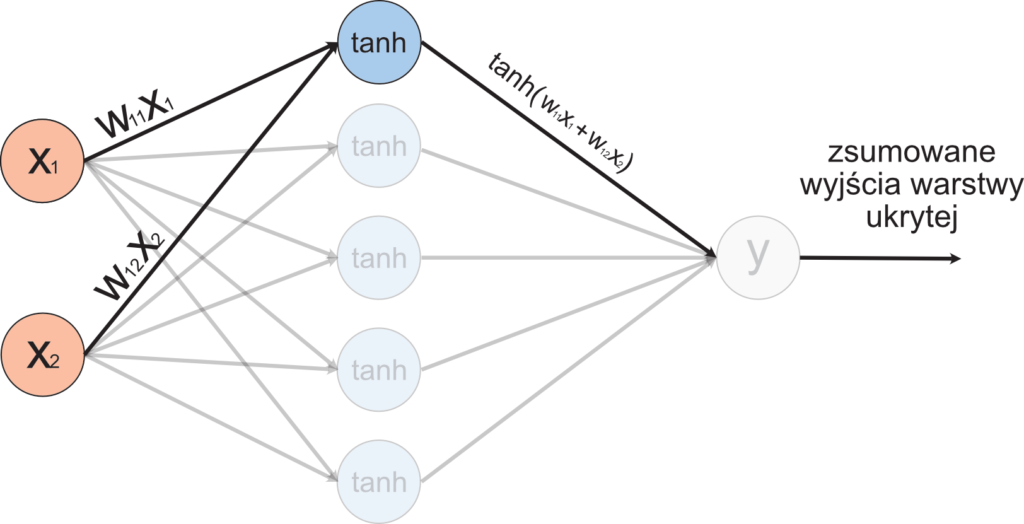
Następną ważną składową naszej sieci jest funkcja aktywacji, która w naszym przypadku jest funkcją równą tangensowi hiperbolicznemu (nn.Tanh()):

Funkcja aktywacji w skrócie służy temu, aby wprowadzić nieliniowość do procesu nauczania sieci, a co za tym idzie, przygotować sieć na nieliniowe problemy. W praktyce jest to najobszerniejsza grupa – śmiało można rzec, że znaczna większość codziennego świata jest nieliniowa, zatem istnieje taka konieczność, aby sieć przygotować na ten fakt.

Wykres funkcji tangensa hiperbolicznego wygląda następująco:

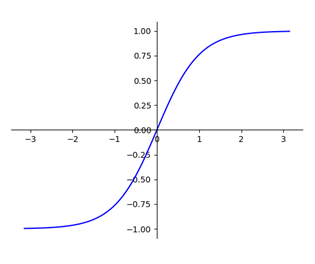
Wartości naszej funkcji aktywacji wchodzą w zakres pomiędzy -1 a 1. Jest to świetna funkcja, która wprowadza poprzez swoją nieliniowość możliwość rozwiązania nieliniowych problemów. W dodatku jest wycentrowaną funkcją, ponieważ dla argumentu zero również przyjmuje wartość równą zeru — przecina osie dokładnie w punkcie (0,0). Z tego powodu, podczas gdy nasza sieć się uczy i próbuje poznać, jak wrażliwa jest funkcja błędu (pomyłki) na wspomniane wcześniej wagi każdego z wejść (licząc gradient tej funkcji), korzysta z przywileju, iż gradient tangensu hiperbolicznego jest symetryczny względem osi zerowej (y = 0).

To wielka przewaga tej funkcji nad wieloma pozostałymi nieliniowymi funkcjami aktywacji. Jednakże różne klasy problemów do rozwiązania mają swoje empiryczne rekomendacje odnośnie zastosowania konkretnej funkcji aktywacji. W internecie możemy spotkać mnóstwo dobrej jakości poradników w tym zakresie i warto z nich korzystać, ponieważ zazwyczaj są one poparte praktyką.

Ostatnią transformacją wiążącą warstwę ukrytą i warstwę wyjściową jest również relacja liniowa. Funkcja forward zdefiniowana w tej samej klasie ma za zadanie przyjąć wektor wejściowy i „przepuścić” go przez kolejne warstwy, po czym zwrócić tensor wyjściowy. Taki tensor jest dla nas po prostu informacją o tym, jaki wynik operacji XOR otrzymamy. Wynikiem będzie liczba zmiennoprzecinkowa pomiędzy 0 a 1, gdyż wynik operacji XOR to właśnie w idealnym przypadku 0 lub 1 – tutaj sieć o tym nie wie, dlatego z pewnym prawdopodobieństwem przybliża się ku zeru lub jedynce, stąd zmiennoprzecinkowość.

W skrócie, cały proces przygotowania oraz treningu naszej sieci będzie przebiegał w następujących krokach:

1. Inicjalizacja klasy odpowiedzialnej za dostarczenie danych treningowych.
2. Pobranie częściowej paczki danych z całościowej kolekcji danych treningowych sieci.
3. Obliczenie przez obecny model sieci wyjścia dla zaprezentowanych danych wejściowych.
4. Obliczenie błędu, czyli różnicy pomiędzy wynikiem oczekiwanym (podanym na przykład przez nas w klasie odpowiedzialnej za dostarczenie danych – będzie to na przykład dla pary liczb (0,1) oczekiwany wynik 1, ponieważ operacja XOR dla tej pary daje właśnie taki wynik) a tym, jaki wynik otrzymaliśmy w punkcie 3.
5. Dokonanie propagacji wstecznej błędu, czyli sprawdzenie na podstawie funkcji gradientu (czyli funkcji prezentującej wrażliwość funkcji błędu na wagi nadane konkretnym wejściom), w którym punkcie jesteśmy (czy zwiększając na przykład wagę danego wejścia zwiększymy, czy zmniejszymy błąd – będziemy zawsze chcieli go zmniejszyć).
6. Aktualizacja wag tak, aby zmniejszyć błąd sieci.
7. Gdy błąd jest na tyle mały, że uznamy go za satysfakcjonujący, zapisujemy model sieci.

Punkty od 2. do 6. będziemy powtarzać cyklicznie aż osiągniemy zadowalającą dokładność przewidywania wyniku przez model sieci.

Przejdźmy zatem do kluczowej części kodu, czyli treningu naszej sieci. W tym celu, posługując się powyższą instrukcją, przeanalizujemy kod, którego zadaniem będzie w ogólności trening naszego modelu sieci. Oto kod klasy Net, której zadaniem jest dostarczenie funkcjonalności trenowania sieci:

Powyższy kod możemy wykorzystać w ten sposób (na przykład z poziomu głównego pliku main.py):

Po wywołaniu powyższego kodu powinniśmy ujrzeć w wyjściu terminala naszego IDE (u mnie VSCode) logi odnośnie kolejnych iteracji treningowych. A oto różnica pomiędzy pierwszą iteracją a ostatnią:

Dużo wygodniejszą formą logowania postępów treningowych naszej sieci jest wykorzystanie zewnętrznych narzędzi, na przykład TensorBoard. Pakiet ten zawarty jest w bibliotece PyTorch, a jego użycie jest niezwykle proste. W tym celu dodamy kilka linii kodu do naszej klasy Net w pliku net.py.

Wszystkie zmiany, poczynając od importu SummaryWriter z pakietu torch.utils.tensorboard powiązane są z nowym obiektem (właśnie wspomnianego typu SummaryWriter) tensorboard_logger w naszej klasie Net. Zadaniem tego obiektu jest zalogowanie danych, w naszym przypadku błędu sieci do wskazanego folderu (u nas to folder logs). Następnie, gdy chcemy zobaczyć wyniki, które zostały zalogowane, wystarczy, że wywołamy w konsoli (na przykład w terminalu naszego VSCode’a) komendę:

tensorboard –logdir logs

Po wywołaniu powyższej komendy zostanie utworzony wirtualny lokalny serwer o podanym adresie, pod którym (na przykład w naszej przeglądarce) będziemy w stanie ujrzeć panel loggera.

Pod adresem http://localhost:6006/ ujrzymy między innymi taki widok:

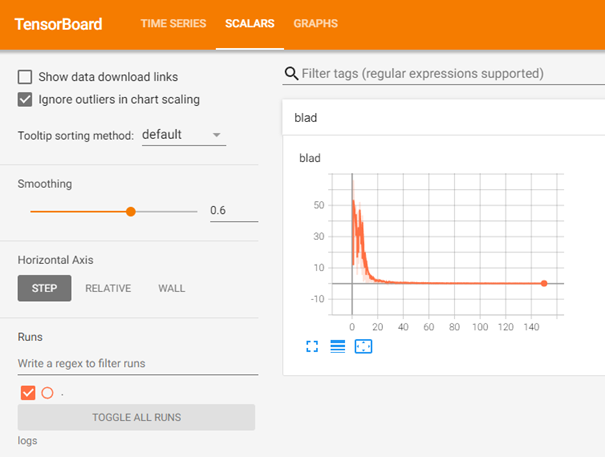
Gdzie na osi horyzontalnej mamy odnotowany numer iteracji, natomiast na osi pionowej błąd w procentach.

Zazwyczaj trening skomplikowanych modeli sieci neuronowych jest czasochłonny – zatem pozostaje pytanie, co można zrobić, aby nie utracić danych treningowych w losowych przypadkach lub aby móc podzielić ten czasochłonny proces na kilka mniejszych? Oczywiście można zapisać parametry tymczasowego modelu do pliku, a następnie wczytać ostatnie zapisane podczas ponownej sesji treningowej. Aby wczytać oraz zapisać stan bieżący modelu, należy użyć wbudowanych metod pakietu torch. Przykład wczytania bieżącego, ostatnio zapisanego modelu oraz zapisanie modelu po ukończeniu treningu sieci zaprezentowany został w poniższym przykładzie wywołania treningu w pliku main.py:

Użycie naszego modelu do uzyskania przewidywanych wartości operacji XOR dla dowolnej pary liczb jest dość banalne i wymaga wywołania przeciążonego operatora () (__call__), to znaczy:

Biblioteka PyTorch ma bardzo szerokie zastosowanie w obszarze przygotowywania modeli sieci neuronowych, ich wykorzystania, a także w obróbce danych z nią związanych. W treningu głębokich sieci neuronowych ważne jest zarówno odpowiednie dobranie parametrów sieci neuronowej, jak i odpowiednie przygotowanie danych treningowych oraz walidacyjnych – ogółem zbioru danych do wykorzystania w procesie.

PyTorch nie jest konieczny w użyciu, gdy chcemy zdefiniować w procesie treningowym model, który będzie wystarczający, lecz zawiera dwie bardzo przydatne funkcjonalności umożliwiające obliczenie gradientu oraz umożliwia dynamiczną kreację grafów, a następnie w prosty sposób – zawołaniem jednej funkcji – propagację wsteczną błędu i aktualizację wag na podstawie tej informacji.

Zakończenie

Mam nadzieję, że ten prosty przykład zobrazuje potrzebę istnienia uczenia maszynowego, a także uczenia głębokiego w obszarach naszego życia codziennego. Obecnie dostępne spektakularne rozwiązania, mające realny wpływ na poprawę życia są wykorzystywane w obszarze medycyny – zarówno szeroko pojętej diagnostyki, jak i do wsparcia zdrowia psychicznego.

PyTorch jest dobrym narzędziem do tego, aby takie szczytne zadania realizować, choć zazwyczaj realizacja skomplikowanych wyzwań w medycynie wymaga nie tylko zespołu wyspecjalizowanych programistów, lecz także ekspertów z zakresu medycyny, chociażby po to, aby nadzorować uczenie takich sieci oraz przygotowanie odpowiednich danych treningowych i walidacyjnych. Jednak my, jako ludzie odpowiedzialni za stronę techniczną tych rozwiązań mamy świetne narzędzia, aby swoją misję realizować, a tym artykułem (mam nadzieję) pomogłem choć jednemu z Was zainteresować się tematem.

Zdjęcie główne artykułu pochodzi z unsplash.com.